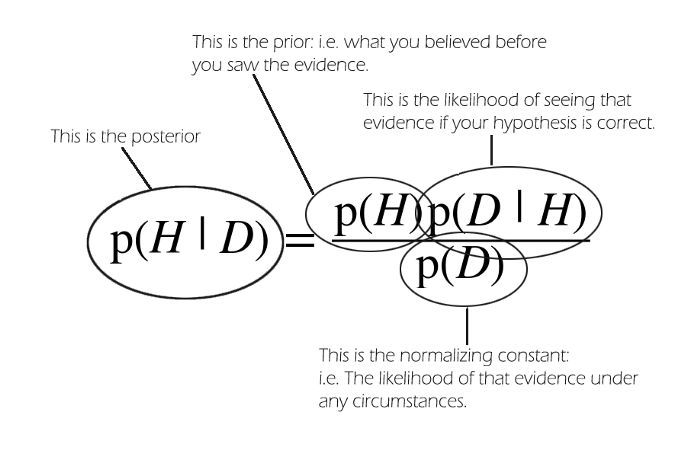
正交性(Orthogonality)
这一章主要介绍正交性相关的内容。包括正交向量,投影,正交子空间,正交基以及如果求一组正交基,最后介绍QR分解求线性方程组。
正交向量(Orthogonal vectors)
给定向量$v,w$,如果$v^T w = 0$,那么这两个向量就是正交向量。
正交子空间(Orthogonal subspaces)
如果对于$\forall v\in V, \forall w\in W$,都有$v^T w = 0$,那么我们称subspaces $V,W$是orthogonal subspaces。
Column space, nullsapce, row space, left nullspace的正交性
-
Row space和nullspace是正交的。
举个例子来证明吧,有$A= \begin{bmatrix}c1&c2\end{bmatrix} = \begin{bmatrix}r1\\r2\end{bmatrix} = \begin{bmatrix}1&1&2&4\\0&0&1&3\end{bmatrix}$
因为row space是row vector的linear combination,即$c_1 r_1+c_2 r_2$,而nullspace是$Ax=0$的所有解,即$x_1 c_1+x_2c_2 = 0$,这里的$0$是向量,可以推出来$r_1x = 0, r_2x =0 $,所以$c_1 r_1 x =0, c_2 r_2x = 0$,也就是说row space中的任意vector和nullspace中的vector都正交。
使用数值方法证明:
$x$表示$Ax=0$中的$x$,$A^Ty$表示row space,那么有
$$x^T (A^T y) = (Ax)^T y = 0^T y = 0$$ -
Column space和nullspace是正交的。
正交补(Orthogonal complements)
定义
如果一个subspace包含所有和subspace $V$正交的向量,称这个subspace是$V$的orthogonal complements(正交补)。
示例
Nullspace是row space的正交补($\mathbb{R}^n$上)。
Left nullspace是column space的正交补($\mathbb{R}^m$上)。
投影(Projections)
如下图所示,左边是投影到一条直线上的结果,右边是投影到一个subspace上的结果

$A^T A$
$A^T A$是可逆的,当且仅当$A$有linear independent columns时
证明:
$A^TA$是一个$n\times n$的方阵,$A$的nullspace和$A^T A$的nullspace相等。
如果$Ax= 0$,那么$A^T Ax = 0$,所以$x$也在$A^T A$的nullspace中。如果$A^T Ax=0$,那么我们要证明$Ax=0$,在左右两边同乘$x^T $得$x^T A^T Ax=0$,则$(AX)^T AX =0$,所以$\vert Ax\vert^2 =0$。也即是说如果$A^T Ax=0$,那么$Ax$的长度为$0$,也就是$Ax=0$。
如果$A^T A$的columns是独立的,也就是说nullspace为空,所以$A$的columns也是独立的;同理,如果$A$的columns是独立的,那么$A^T $的columns也是独立的。
最小二乘法(Least Squares Approximations)
$Ax=b$无解的情况,通常是等式个数大于未知数的个数,即$m\gt n$,$b$不在$A$的column space内。我们的目标是想让$e=b-Ax$为$0$,当这个目标不能实现的时候,可以在方程左右两边同时乘上$A^T$,求出一个近似的$\hat{x}$:
$$A^TAx = A^Tb$$
如何推导出这个结果,有以下几种方法:
最小化误差
-
几何上
$Ax=b$的最好近似是$A\bar{x} = p$,最小的可能误差是$e=b-p$,$b$上的点的投影都在$p$上,而$p$在$A$的column space上,从直线拟合的角度上来看,$\bar{x}$给出了最好的结果。 -
代数上
$b=p+e$,$e$在$A$的nullspace上,$Ax=b=p+e$我们解不出来,$A\bar{x} = p$我们可以解出来。 -
积分
直线拟合
抛物线拟合
正交基(Orthogonal Bases)
定义
一组向量$q_1, q_2, \cdots , q_n$如果满足以下条件:
$$q_i^T q_j\begin{cases}0, i\neq j \\1, i=j\end{cases}$$
我们称这一组向量是正交向量,由正交column vectors构成的矩阵用一个特殊字母$Q$表示。如果这组正交向量同时还是单位向量,我们叫它单位正交向量。如果columns仅仅正交,而不是单位向量的话,点乘仍然会得到一个对角矩阵,但是它的性质没有那么好。
性质
- 满足$Q^T Q=I$。
- 如果$Q$是方阵,那么$Q^T = Q^{-1}$,即转置等于逆。
- 如果$Q$是方阵的话,$QQ^T = Q^T Q= I$。
- 如果$Q$是rectangular的话,$QQ^T =I$不成立,而$Q^T Q =I$依然成立。
用$Q$取代$A$进行正交投影
假设矩阵$A$的所有column vectors都是orthonormal的,$a$就变成了$q$,$A^T A$就变成了$Q^T Q=I$,所以$Ax=b$的解变成了$\bar{x} = Q^T b$,而投影矩阵变成了$P=QQ^T $。
Gram-Schmidi正交化
Gram-Schmidt正交化过程就相当于是在不断的进行投影,这个方法的想法是从$n$个独立的column vector出发,构建$n$个正交向量,然后再单位化。拿$3$个过程举个例子。用$a,b,c$表示初始的$3$个独立向量,$A,B,C$表示三个正交向量,$q_1, q_2,q_3$表示三个正交单位向量。
第一个正交向量,直接对第一个向量单位化
$$A=a, q_1 = \frac{A}{\vert A\vert}$$
第二个正交向量,将第二个向量投影到第一个向量上,计算出一个和第二个向量正交的向量。
$$B=b-\frac{A^T B}{A^T A}A , q_2 = \frac{B}{\vert B\vert}$$
第三个正交向量,将第三个向量分别投影到第一个和第二个正交向量上,计算处第三个正交向量。
$$C=c - \frac{A^T C}{A^T A}A - \frac{B^T C}{B^T B}B , q_2 = \frac{C}{\vert C\vert}$$

QR分解
假设一个矩阵$A$的列向量分别为$a,b,c$,最后经过一个三角矩阵$R$化简成一个正交矩阵$Q$,相应的列向量分别为$q_1,q_2,q_3$。
首先根据Gram-Schmidi计算处一组正交基$Q = \begin{bmatrix}q_1&q_2&q_3 \end{bmatrix}$。根据$A$,能直接计算出$Q$,那么如何得到$R$呢?我们假设$A=QR$,在$A$和$Q$已知的情况下,并且满足$Q^T Q = I$,我们可以左右两边同时乘上$Q^T $,就有$Q^T A = Q^T QR = R$,即$R=Q^T A$。
参考文献
1.MIT线性代数公开课