logistic regression
逻辑回归是使用线性模型进行分类的模型,它是一个对数线性模型。
在使用线性模型进行回归时,产生的预测值是实数值。而对于分类任务,函数的输出需要是离散值。对于二分类任务,类别分别记为$0$和$1$,如果将回归模型的值限制在$[0, 1]$之间,那么接下来我们要做的就是将$[0,1]$之间的值转换为$0$和$1$。比如单位跃阶函数:
$$y=\begin{cases}0, x \lt 0;\\0.5, x=0;\\1, x\gt 0\end{cases} \tag{1}$$
但是它是离散的,需要找一个连续的函数。这就是接下来介绍的logistic function。
logistic distribution
连续随机变量$X$服从logistic distribution指的是$X$具有以下分布函数和密度函数:
$$F(x) = P(X\le x) = \frac{1}{1 + e^{-(x-\mu)/\gamma} } \tag{2}$$
$$f(x) = F’(x) = \frac{e^{-(x-\mu)/\gamma} }{\gamma(1 + e^{-(x-\mu)/\gamma} )^2 } \tag{3}$$
其中$\mu$为位置参数,$\gamma \gt 0$是形状参数。分布函数属于logistic function,相应的图如下所示,它的取值在$[0,1]$之间,是一条sigmod曲线,以点$(\mu, \frac{1}{2})$为中心对称,即满足:
$$F(-x+\mu) - \frac{1}{2} = -F(x-\mu) +\frac{1}{2} \tag{4}$$
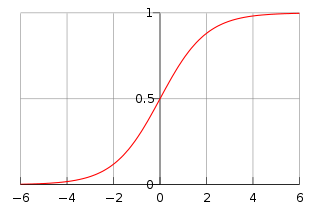
曲线在中心附近增长的速度很快,在两端增加的速度很慢。$\gamma$越小,曲线在中心附近增长的越快。当$\mu=0, \gamma=1$时,得到一个特殊的函数:
$$ f(x) = \frac{1}{1+e^{-x} } \tag{5}$$
用$w^T x+b$代替$f(x)$中的$x$,就得到了:
$$h(x) = \frac{1}{1+ e^{-(w^T x +b)} } \tag{6}$$
其中$x$是输入,$\theta$是要求的参数。
二项logistic regression
上面给出的$y=h(x)$其实是一个二项的logistic regression分类函数。式子$(6)$可以进行变形,得到
$$ \log\frac{y}{1-y} = \log\frac{\frac{1}{1+ e^{-(w^T x +b)} } }{1-\frac{1}{1+ e^{-(w^T x +b)} } }= \log\frac{\frac{1}{1+ e^{-(w^T x +b)} } }{\frac{e^{-(w^T x +b)} }{1+ e^{-(w^T x +b)} } } = \log\frac{1}{e^{-(w^T x +b) } } = w^T x +b \tag{7}$$
这里的$y$是一个函数值,给定一个$x$就会有一个$y$。将$y$看做给定$x$,事件发生的概率,$1-y$是该事件不发生的概率,两者的比值$\frac{y}{1-y}$被称为几率,反映了$x$发生的相对可能性。对几率取对数得到对数几率logit:
$$\log \frac{y}{1-y}$$
可以看出,公式$6$实际上是在近似真实标记的对数几率。所以这个模型叫作对数几率回归。如果将式子$(6)$中的$y$看成类后验概率估计$p(y=1|x)$,公式$(7)$可以写成:
$$\log \frac{p(y=1|x)}{p(y=0|x)} = w^T x+b \tag{8}$$
则有:
$$ p(y=1|x) = \frac{e^{w^T x+ b} }{1+e^{w^T x+ b} } \tag{9} $$
$$ p(y=0|x) = \frac{1}{1+e^{w^T x+ b} } \tag{10} $$
其实就是分子分母同时乘了$e^{w^T x+ b}$。线性模型$w^T x+b$的值域是实数域,然而logistic模型将线性函数$w^T x+b$转换成了如公式$(8),(9)$的概率。当$w^T x+b$的值越接近于$1$,$p(y=1|x)$的概率越接近于$1$。
最大似然估计进行参数估计
给定训练集样本$(x_1, y_1), \cdots, (x_N,y_N)$,可以使用最大似然估计求解给定的$w$和$b$:
$$l(w,b) =\prod_{i=1}^m p(y_i|x_i; w,b) \tag{11}$$
即让所有样本属于其真实标记的概率越大越好。设$p(y=1|x) = \pi(x), p(y=0|x) = 1-\pi(x)$,这两个式子可以用一个式子表示$\pi(x)^y (1-\pi(x))^{1-y} $,重写式子$(11)$,得到的似然函数为:
$$l(w,b) =\prod_{i=1}^m p(y_i|x_i; w,b) = \prod_{i=1}^m \left[\pi(x)\right]^{y_i} \left[1-pi(x)\right]^{1-y_i} \tag{12}$$
取对数得到对数似然:
\begin{align*}
L &= \log l(w,b) \\
& = \log \prod_{i=1}^m \left[\pi(x)\right]^{y_i} \left[1-pi(x)\right]^{1-y_i}\\
& = \sum_{i=1}^m \left[y_i\log\pi(x)+(1-y_i)\log(1-\pi(x_i)) \right] \tag{13}\\
& = \sum_{i=1}^m \left[y_i\log\frac{\pi(x)}{1-\pi(x_i)} + \log(1-\pi(x_i)) \right] \tag{14}\\
& = \sum_{i=1}^m \left[y_i (w^T x+b) - \log(1+e^{w^T x+b} ) \right]\\ \tag{15}
\end{align*}
然后求得$w$和$b$即可。
多项logistic regression
假设离散型随机变量的取值集合是${1, 2,\cdots, K}$,多项logistic regression的公式是:
$$P(Y=k|x) = \frac{e^{w^T x+b} }{ 1+ \sum_{k=1}^{K-1} e^{w^T x+b} }, k = 1, 2, \cdots, K-1 \tag{16}$$
$$P(Y=K|x) = \frac{1}{1+ \sum_{k=1}^{K-1} e^{w^T x+b} } \tag{17}$$
参考文献
1.周志华《西瓜书》
2.李航《统计机器学习》