C/C++ IEEE 754 Floating Point Standard

小数转二进制

0.8125转换为二进制小数。

0.8125
x 2
1.6250  取整数部分1
0.6250
x 2
1.25    取整数部分1
0.25
x 2
0.5     取整数部分0
x 2
1.0     取整数部分1
最后得到1101，再加上小数点即0.1101

分数转二进制

将分数转换成小数。
下面的做法只针对于这一个，对于其他的一些并不简单。
$15/32$转换为二进制小数？？这个是不是有问题，如果分母是28怎么算？？？
分开来算，
$15 = (1111)_2 = 2^3 + 2^2 + 2^1 + 2^0 $
$32 = (100000)_2 = 2^5 $
即
$15/32 = 2^{-2} + 2^{-3} + 2^{-4} + 2^{-5} $
而$2^{-2} = 0.01, 2^{-3} = 0.001, 2^{-4} = 0.0001, 2^{-5} = 0.00001 $
所以$15/32 = 0.01111$

浮点数

浮点数使用科学计数法表示实数，一个尾数(Mantissa)，一个基数（Base），一个指数（Exponent）以及一个表示正负的符号来表达实数。比如 123.45 用十进制科学计数法可以表达为 1.2345 × 102 ，其中 1.2345 为尾数，10 为基数，2 为指数。浮点数利用指数达到了浮动小数点的效果，从而可以灵活地表达更大范围的实数。
有很多方法表示浮点数，IEEE 754是最有效的方法。在IEEE标准中，浮点数由符号域，指数域，尾数域组成。

The Sign of Manitissa（符号域）：0代表正数，1代表负数
The Biased exponent（有偏指数域）：指数域是有一个biased的。
The normalised Mantisa（尾数）：有效数字
通过调整尾数和指数就可以表达不同的数值。具体格式如下：

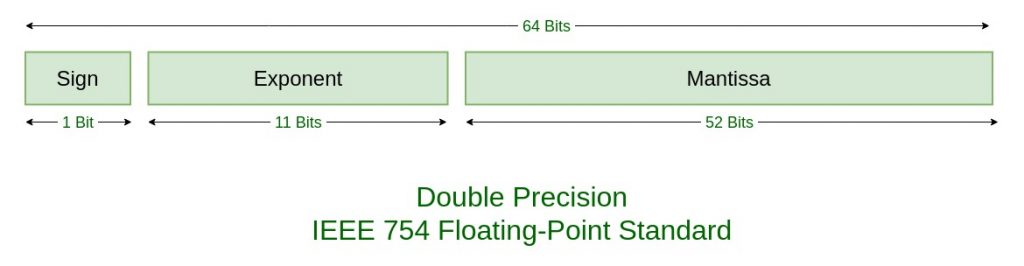
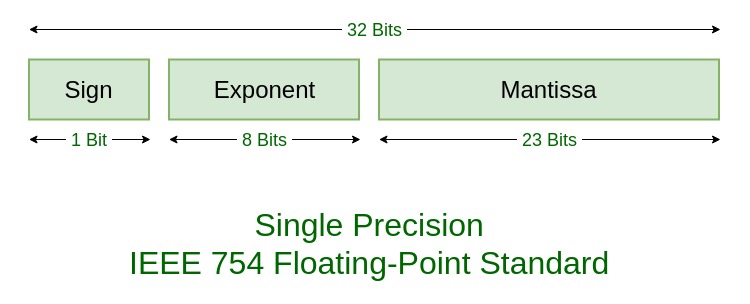
类型	符号位	有偏指数域	尾数域	偏置
单精度	第31位	第30-23位	第22-0位	127
双精度	第63位	第62-52位	第52-0位	1023

示例

85.125 
先转换为二进制，然后计算符号域，指数域和尾数域。
0.125 = 001
85.125 = 1010101.001
       =1.010101001 x 2^6 
sign = 0 

1. Single precision:
有偏指数：
biased exponent 127+6=133
133 = 10000101
规范化的尾数：
Normalised mantisa = 010101001
we will add 0's to complete the 23 bits

The IEEE 754 Single precision is:
= 0 10000101 01010100100000000000000
This can be written in hexadecimal form 42AA4000

2. Double precision:
biased exponent 1023+6=1029
1029 = 10000000101
Normalised mantisa = 010101001
we will add 0's to complete the 52 bits

The IEEE 754 Double precision is:
= 0 10000000101 0101010010000000000000000000000000000000000000000000
This can be written in hexadecimal form 4055480000000000

参考文献

1.https://www.cnblogs.com/xiabodan/p/4038623.html
2.https://www.geeksforgeeks.org/ieee-standard-754-floating-point-numbers/
3.https://www.cnblogs.com/xkfz007/articles/2590472.html
4.https://www.cnblogs.com/weixuqin/p/7086442.html
5.http://cs.furman.edu/digitaldomain/more/ch6/dec_frac_to_bin.htm