MM
MM是一类迭代优化方法,利用函数的凸性寻找极大值或者极小值。MM是Majoriza-Minimization或者Minorize-Maximization的缩写,取决于优化目标是maximization还是minimization。MM不是一个算法,它描述了如何如构建一个优化算法。
EM算法可以看成MM算法的一个例子。但是EM算法使用到了条件期望,而MM算法中凸性和不等式是重点。
算法思路
MM算法寻找objective function的一个替代品,然后优化新的目标函数直到一个极值点。
拿minorize-maximization算法举个例子,用$f(\theta)$表示需要被maximized的目标函数,它是一个concave函数。在第$m=0,1,\cdots$步中,构建新的目标函数$g(\theta|theta_m)$满足:
$$g(\theta|\theta_m) \le f(\theta), \forall \theta \tag{1}$$
$$g(\theta_m|\theta_m) = f(\theta_m) \tag{2}$$
式子$(1)表示$g(\theta|\theta_m)$是$f(\theta)$的下界,式子$(2)$表明$f(\theta)$和$g(\theta|\theta_m)$可以取到等号。
如下图所示:
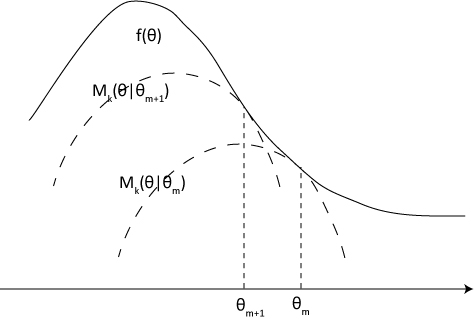
接下来,通过最大化$g(\theta|\theta_m)$就可以最大化$f(\theta)$:
$$\theta_{m+1} = \arg \max_{\theta} g(\theta|\theta_m) \tag{3}$$
当$m\rightarrow \infty$时,$f(\theta_m)$就会收敛到极小值点或者鞍点。我们能够得到以下的几个关系式:
$$f(\theta_{m+1}) \ge g(\theta_{m+1}|\theta_m) \ge g(\theta_m|\theta_m)=f(\theta_m) $$