gradient method trust region policy optimization

Trust Region Policy Optimization

作者提出了optimizing policies的一个迭代算法，理论上保证可以以non-trivial steps单调改善plicy。对经过理论验证的算法做一些近似，产生一个实用算法，叫做Trust Region Policy Optimization(TRPO)。这个算法和natural policy gradient很像，并且在大的非线性网络优化问题上有很高的效率。TRPO有两个变种，single-path方法应用在model-free环境中，vine方法，需要整个system能够能够从特定的states重启，通常在仿真环境中可用。

Introduction

为什么要有TRPO？

policy gradient计算的是expected rewards梯度的最大方向，然后朝着这个方向更新policy的参数。因为梯度使用的是一阶导数，梯度太大时容易fail，梯度太小的话更新太慢。
学习率很难选择，学习率固定，梯度大容易失败，梯度小更新太慢。
如何限制policy，防止它进行太大的move。然后如何将policy的改变转换到model parameter的改变上。
采样效率很低。对整个trajectory进行采样，但是仅仅用于一次policy update。在一个trajectory中的states是很像的，尤其是用pixels表示时。如果在每一个timestep都改进policy的话，会一直在某一个局部进行更新，训练会变得很不稳定。

Motivation

我们想要每一次策略$\pi$的更新，都能使得$\eta(\pi)$单调递增。要是能将它写成old poliy $\pi_{old}$和new policy $\pi_{new}$的关系式就好啦。给出这样一个关系式：
$$\eta(\pi_{new}) = \eta(\pi_{old}) + \mathbb{E}_{s_0, a_0, \cdots \sim \pi_{new}} \left[\sum_{t=0}^{\infty} \gamma^t A^{\pi_{old}}(s_t,a_t)\right] \tag{1}$$
证明：
\begin{align*}
\mathbb{E}_{s_0, a_0,\cdots\sim \pi_{new} }\left[\sum_{t=0}^{\infty} \gamma^t A^{\pi_{old}} (s_t,a_t) \right] &=\mathbb{E}_{s_0, a_0,\cdots\sim \pi_{new}}\left[\sum_{t=0}^{\infty} \gamma^t (Q^{\pi_{old}} (s_t,a_t) - V^{\pi_{old}} (s_t))\right] \\
&=\mathbb{E}_{s_0, a_0,\cdots\sim \pi_{new}} \left[\sum_{t=0}^{\infty} \gamma^t ( R_{t+1} + \gamma V^{\pi_{old}} (s_{t+1}) - V^{\pi_{old}} (s_t))\right] \\
&=\mathbb{E}_{s_0, a_0,\cdots\sim \pi_{new}} \left[\sum_{t=0}^{\infty} \gamma^t R_{t+1} + \sum_{t=0}^{\infty} \gamma^t (\gamma V^{\pi_{old}} (s_{t+1}) - V^{\pi_{old}} (s_t))\right] \\
&=\mathbb{E}_{s_0, a_0,\cdots\sim \pi_{new}} \left[\sum_{t=0}^{\infty} \gamma^t R_{t+1} \right]+ \mathbb{E}_{s_0, a_0,\cdots\sim \pi_{new}} \left[\sum_{t=0}^{\infty} \gamma^t (\gamma V^{\pi_{old}} (s_{t+1}) - V^{\pi_{old}} (s_t))\right] \\
&=\eta(\pi_{new}) + \mathbb{E}_{s_0, a_0,\cdots\sim \pi_{new}} \left[ - V^{\pi_{old}} (s_0))\right] \\
&=\eta(\pi_{new}) - \mathbb{E}_{s_0, a_0,\cdots\sim \pi_{new}} \left[ V^{\pi_{old}} (s_0))\right] \\
&=\eta(\pi_{new}) - \eta(\pi_{old})\\
\end{align*}
将new policy $\pi_{new}$的期望回报表示为old policy $\pi_{old}$的期望回报加上另一项，只要保证这一项是非负的即可。其中$\mathbb{E}_{s_0, a_0,\cdots, \sim \pi_{new}}\left[\cdots\right]$表示actions是从$a_t\sim\pi_{new}(\cdot|s_t)$得到的。

用求和代替期望

代入$s$的概率分布$\rho_{\pi}(s) = P(s_0 = s) +\gamma P(s_1=s) + \gamma^2 P(s_2 = s)+\cdots, s_0\sim \rho_0$，并将期望换成求和：
\begin{align*}
\eta(\pi_{new}) &= \eta(\pi_{old}) + \mathbb{E}_{s_0, a_0, \cdots \sim \pi_{new}} \left[\sum_{t=0}^{\infty} \gamma^t A^{\pi_{old}}(s_t,a_t)\right]\\
&=\eta(\pi_{old}) +\sum_{t=0}^{\infty} \sum_s P(s_t=s|\pi_{new}) \sum_a \pi_{new}(a|s)\gamma^t A^{\pi_{old}}(s,a)\\
&=\eta(\pi_{old}) +\sum_s\sum_{t=0}^{\infty} \gamma^t P(s_t=s|\pi_{new}) \sum_a \pi_{new}(a|s)A^{\pi_{old}}(s,a)\\
&=\eta(\pi_{old}) + \sum_s \rho_{\pi_{new}}(s) \sum_a \pi_{new}(a|s) A^{\pi_{old}} (s,a) \tag{2}\\
\end{align*}
从上面的推导可以看出来，任何从$\pi_{old}$到$\pi_{new}$的更新，只要保证每个state $s$处的expected advantage是非负的，即$\sum_a \pi_{new}(a|s) A_{\pi_{old}}(s,a)\ge 0$，就能说明$\pi_{new}$要比$\pi_{old}$好，在$s$处，新的policy $\pi_{new}$:
$$\pi_{new}(s) = \arg\ \max_a A^{\pi_{old}} (s,a) \tag{3}$$
直到所有$s$处的$A^{\pi_{old}} (s,a)$为非正停止。当然，在实际应用中，因为各种误差，可能会有一些state的expected advantage是负的。

$\rho_{\pi_{old}}(s)$近似$\rho_{\pi_{new}}(s)$（第一次近似）

式子$(2)$中包含的$\rho_{\pi_{new}}$依赖于未知的$\pi_{new}$，而我们已知的是$\pi_{old}$，忽略因为policy改变导致的state访问频率的改变，在$L_{\pi_{old}}(\pi_{new} )$中用$\rho_{\pi_{old}}(s)$近似$\rho_{\pi_{new}}(s)$。
\begin{align*}
\eta(\pi_{new}) &= \eta(\pi_{old}) + \sum_s\rho_{\pi_{new}}(s)\sum_a\pi_{new}(a|s)A^{\pi_{old}} (s,a)\\
& = \eta(\pi_{old}) + \mathbb{E}_{s\sim \pi_{new}, a\sim \pi_{new}}A^{\pi_{old}}(s,a)\\
& = \eta(\pi_{old}) + \mathbb{E}_{s\sim \pi_{new}, a\sim \pi_{old}}\left[\frac{\pi_{new}(a|s)}{\pi_{old}(a|s)}A^{\pi_{old}}(s,a)\right]\tag{4}\\
\end{align*}

\begin{align*}
L_{\pi_{old}}(\pi_{new}) & = \eta(\pi_{old}) + \sum_s\rho_{\pi_{old}}(s)\sum_a\pi_{new}(a|s)A^{\pi_{old}} (s,a)\\
& = \eta(\pi_{old}) +\mathbb{E}_{s\sim \pi_{old}, a\sim \pi_{new}}A^{\pi_{old}}(s,a)\\
& = \eta(\pi_{old}) +\mathbb{E}_{s\sim \pi_{old}, a\sim \pi_{old}}\left[\frac{\pi_{new}(a|s)}{\pi_{old}(a|s)}A^{\pi_{old}}(s,a)\right]\tag{5}\\
\end{align*}

用$\pi_{\theta}(a|s)$表示可导policy，用$\theta_{old}$表示$\pi_{old}$的参数。当$\pi_{new} = \pi_{old}$时，即$\theta=\theta_{old}$时，$L_{\pi_{old}}(\pi_{new})$和$\eta(\pi_{new})$的一阶导相等：
$$L_{\pi_{old}}(\pi_{new}) = \eta(\pi_{old}) + \sum_s\rho_{\pi_{old}}(s)\sum_a\pi_{old}(a|s)A^\pi_{old}(s,a) = \eta(\pi_{new})\tag{6}$$
$$\nabla_{\theta} L_{\pi_{old}}(\pi_{new})|_{\theta=\theta_{old}} = \mathbb{E}_{s\sim \pi_{old}, a\sim \pi_{old}}\left[\frac{\nabla_{\theta}\pi_{new}(a|s)}{\pi_{old}(a|s)}A^{\pi_{old}}(s,a)\right]|_{\theta_{old}}\tag{7} $$
$$\nabla_{\theta} \eta(\pi_{new})|_{\theta=\theta_{old}} =\mathbb{E}_{s\sim \pi_{new}, a\sim \pi_{old}}\left[\nabla_{\theta}\log\pi_{new}(a|s)A^{\pi_{old}}(s,a)\right]|_{\theta_{old}} \tag{8}$$
证明：
式子$(6)$将$\pi_{new}=\pi_{old}$代入即可。我对于式子$7$和$8$相等有疑问，为什么？
也就是说当$\pi_{new} = \pi_{old}$时，$L_{\pi_{old}}(\pi_{new})$和$\eta(\pi_{new})$是相等的，在$\pi_{old}$对应的参数$\theta$周围的无穷小范围内，可以近似认为它们依然相等，$\theta$进行足够小的step更新到达新的policy $\pi_{new}$，相应参数为$\theta_{\pi_{new}}$，在改进$L_{\pi_{old}}$同时也改进了$\eta$，但是这个足够小的step是多少是不知道的。

conservative policy iteration

为了求出这个step到底是多少，有人提出了conservative policy iteration算法，该算法提供了$\eta$提高的一个lower bound。用$\pi_{old}$表示current policy，用$\pi’$表示使得$L_{\pi_{old}}$取得最大值的policy，$\pi’ = \arg\ \min_{\pi’} L_{\pi_{old}}(\pi’)$，新的policy $\pi_{new}$定义为：
$$\pi_{new}(a|s) = (1-\alpha) \pi_{old}(a|s)+\alpha\pi’(a|s) \tag{9}$$
可以证明，新的policy $\pi_{new}$和老的policy $\pi_{old}$之间存在以下关系：
$$\eta(\pi_{new})\ge L_{\pi_{old}}(\pi_{new}) - \frac{2\epsilon \gamma}{(1-\gamma(1-\alpha))(1-\gamma)}\alpha^2 $$
$$\epsilon = \max_s \vert\mathbb{E}_{a\sim\pi’}\left[A^{\pi} (s,a)\right]\vert \tag{10}, \alpha,\gamma\in [0,1]$$
证明：
进行缩放得到：
$$\eta(\pi_{new})\ge L_{\pi_{old}}(\pi_{new}) - \frac{2\epsilon \gamma}{(1-\gamma)^2 }\alpha^2 \tag{11}$$

通用随机策略单调增加的证明

从公式$9$我们可以看出来，改进右边就一定能改进真实的performance $\eta$。然而，这个bound只适用于通过公式$7$生成的混合policy，在实践中，这类policy很少用到，而且限制条件很多。所以我们想要的是一个适用于任何stochastic policy的lower bound，通过提升这个bound提升$\eta$。
作者使用$\pi_{old}$和$\pi_{new}$之间的一个距离代替$\alpha$，将公式$8$扩展到了任意stochastic policy，而不仅仅是混合policy。这里使用的distance measure，叫做total variation divergence，对于离散的概率分布$p,q$来说，定义为：
$$D_{TV}(p||q) = \frac{1}{2} \sum_i \vert p_i -q_i \vert \tag{12}$$
定义$D_{TV}^{max}(\pi_{old}, \pi_{new})$为：
$$D_{TV}^{max} (\pi_{old}, \pi_{new}) = \max_s D_{TV}(\pi_{old}(\cdot|s) || \pi_{new}(\cdot|s))\tag{13}$$
让$\alpha = D_{TV}^{max}(\pi_{old}, \pi_{new})$，新的bound如下：
$$\eta(\pi_{new})\ge L_{\pi_{old}}(\pi_{new}) - \frac{4\epsilon \gamma}{(1-\gamma)^2 }\alpha^2 , \qquad\epsilon = \max_{s,a} \vert A^{\pi_{old}}(s,a)\vert \tag{14}$$
证明：
…

Total variation divergence和KL散度之间有这样一个关系：
$$D_{TV}(p||q)^2 \le D_{KL}(p||q) \tag{15}$$
证明：
…
让
$$D_{KL}^{max}(\pi_{old}, \pi_{new}) = \max_s D_{KL}(\pi_{old}(\cdot|s)||\pi_{new}(\cdot|s)) \tag{16}$$
从公式$12$中可以直接得到：
\begin{align*}
\eta(\pi_{new}) &\ge L_{\pi_{old}}(\pi_{new}) - \frac{4\epsilon \gamma}{(1-\gamma)^2 }\alpha^2 \\
&\ge L_{\pi_{old}}(\pi_{new}) - \frac{4\epsilon \gamma}{(1-\gamma)^2 }D_{KL}^{max}(\pi_{old}, \pi_{new}) \\
& \ge L_{\pi_{old}}(\pi_{new}) - CD_{KL}^{max}(\pi_{old}, \pi_{new})\\
C & =\frac{4\epsilon \gamma}{(1-\gamma)^2} \tag{17}
\end{align*}
根据公式$12$，我们能生成一个单调非递减的sequence：$\eta(\pi_0)\le \eta(\pi_1) \le \eta(\pi_2) \le \cdots$，记$M_i(\pi) = L_{\pi_i}(\pi) - CD_{KL}^{max}(\pi_i, \pi)$，有：
因为：
$$\eta(\pi_{i+1}) \ge M_i(\pi_{i+1})\tag{18}$$
$$\eta(\pi_i) = M_i(\pi_i)\tag{19}$$
上面的第一个式子减去第二个式子得到：
$$\eta(\pi_{i+1}) - \eta(\pi_i)\ge M_i(\pi_{i+1})-M_i(\pi_i) \tag{20}$$
在每一次迭代的时候，确保$M_i(\pi_{i+1}) - M_i(\pi_i)\ge 0$就能够保证$\eta$是非递减的，最大化$M_i$就能实现这个目标，$M_i$是miorize $\eta$的近似目标。这种算法是minorizaiton maximization的一种。

参数化策略的优化（第二次近似）

前面几小节考虑的optimization问题时没有考虑$\pi$的参数化，并且假设所有的states都可以被evaluated。这一节介绍如何在有限的样本下和任意的参数化策略下，从理论基础推导出一个实用的算法。
用$\theta$表示参数化策略$\pi_{\theta}(a|s)$的参数$\theta$，将目标表示成$\theta$而不是$\pi$的函数，即用$\eta(\theta)$表示原来的$\eta(\pi_\theta)$，用$L_{\theta}(\hat{\theta})$表示$L_{\pi_{\theta}}(\pi_{\hat{\theta}})$，用$D_{KL}(\theta||\hat{\theta})$表示$D_{KL}(\pi_{\theta}||\pi_{\hat{\theta}})$。用$\theta_{old}$表示我们想要改进的policy参数。
上一小节我们得到$\eta(\theta) \ge L_{\theta_{old}}(\theta) - CD_{KL}^{max}(\theta_{old}, \theta)$，当$\theta = \theta_{old}$时取等。通过最大化等式右边，可以提高$\eta$的下界：
$$\max_{\theta}\left[L_{\theta_{old}}(\theta) - CD_{KL}^{max}(\theta_{old}, \theta)\right]\tag{21}$$
在实践中，如果使用上述理论中的penalty coefficient $C$，会导致steps size很小。一种方法是使用new policy 和old policy之间的KL散度进行约束，可以采取更大的steps，这个约束叫做trust region constraint:
$$\max_{\theta} L_{\theta_{old}} (\theta)$$
$$ s.t. D_{KL}^{max}(\theta_{old},\theta) \le \delta \tag{22}$$
这样会在state space的每一个state都有一个KL散度约束。由于约束太多，这个问题还是不能解。这里使用average KL divergence进行近似:
$$\bar{D}_{KL}^{\rho}(\theta_1, \theta_2) = \mathbb{E}_{s\sim \rho}\left[D_{KL}(\pi_{\theta_1}(\cdot|s) || \pi_{\theta_2}(\cdot|s))\right] \tag{23}$$
公式$22$变成：
$$\max_{\theta} L_{\theta_{old}} (\theta)$$
$$s.t. \bar{D}_{KL}^{\rho_{\theta_{old}}}(\theta_{old},\theta) \le \delta \tag{24}$$

目标函数和约束的采样估计（第三次近似）

上一节介绍的是关于policy parameter的有约束优化问题，约束条件为每一次policy更新时限制policy变化的大小，优化expected toral reward $\eta$的一个估计值。这一节使用Monte Carlo仿真近似目标和约束函数。
代入$L_{\theta_{old}}$的等式，得到：
$$\max_{\theta}\sum_s \rho_{\theta_{old}}(s) \sum_a\pi_{\theta}(a|s)A_{\theta_{old}}(s,a)$$
$$s.t. \bar{D}_{KL}^{\rho_{\theta_{old}}}(\theta_{old},\theta) \le \delta \tag{25}$$
首先用期望$\frac{1}{1-\gamma}\mathbb{E}_{s\sim \rho_{\theta_{old}}}\left[\cdots\right]$代替目标函数中的$\sum_s\rho_{\theta_{old}}(s) \left[\cdots\right]$。接下来用$Q$值$Q_{\theta_{old}}$代替advantage $A_{\theta_{old}}$，结果多了一个常数项，不影响。最后使用importance smapling代替actions上的求和。使用$q$表示采样分布，$q$分布中单个的$s_n$对于loss函数的贡献在于：
$$\sum_a \pi_{\theta}(a|s_n) A_{\theta_{old}}(s_n,a) = \mathbb{E}_{a\sim q}\left[\frac{\pi_{\theta} (a|s_n) }{q(a|s_n)}A_{\theta_{old}}(s_n,a) \right]\tag{26}$$
上面的公式就是使用importance sampling代替求和。将$A$展开：
\begin{align*}
\sum_a \pi_{\theta}(a|s) A_{\theta_{old}}(s,a) &= \sum_a \pi_{\theta}(a|s)\left( Q_{\theta_{old}}(s,a) - V_{\theta_{old}}(s)\right)\\
&= \sum_a \pi_{\theta}(a|s)Q_{\theta_{old}}(s,a)- \sum_a \pi_{\theta}(a|s)V_{\theta_{old}}(s)\\
&= \sum_a \pi_{\theta}(a|s)Q_{\theta_{old}}(s,a)- V_{\theta_{old}}(s)\\
\end{align*}
将公式$25$的优化问题转化为：
$$\max_{\theta} \mathbb{E}_{s\sim\rho_{\theta_{old}}, a\sim q}\left[\frac{\pi_{\theta} (a|s) }{q(a|s)}Q_{\theta_{old}}(s,a)\right]$$
$$s.t. \mathbb{E}_{s\sim \rho_{\theta_{old}}}\left[D_{KL}(\pi_{\theta_{old}}(\cdot|s)||\pi_{\theta}(\cdot|s))\right]\le \delta \tag{27}$$
好了，前面给出各种证明和近似，终于给出了我们要解决的问题的数学公式，这部分是为了帮助我们理解。我们实际需要的是解这个有约束的优化问题，这也是代码中要实现的部分，具体怎么做，一句话，采样然后估计。用采样代替期望，用经验估计代替$Q$值。
介绍两种方法进行估计。第一个叫做single path，通常用在policy gradient estimation，基于单个轨迹的采样。第二个叫做vine，构建一个rollout set，从rollout set的每一个state处执行多个actions。这种方法经常用在policy iteration方法上。

Single Path

采样$s_0\sim \rho_0$，模拟policy $\pi_{\theta_{old}}$一些timesteps生成一个trajectory $s_0, a_0, s_1, a_1, \cdots, s_{T-1}, a_{T-1}, s_T$，因此$q(a|s) = \pi_{\theta_{old}}(a|s)$。根据trajectory对每一个state action pair $(s_t,a_t)$计算$Q_{\theta_{old}}(s,a)$。

Vine

采样$s_0\sim \rho_0$，模拟policy $\pi_{\theta_i}$生成一系列trajectories。在这些trajectories选择一个具有$N$个states的子集，表示为$s_1, c\dots, s_N$，这个集合称为rollout set。对于rollout set中的每一个state $s_n$，根据$a_{n,k}\sim q(\cdot|s_n)$采样$K$个actions。任何$q(\cdot|s_n)$都行，在实践中，$q(\cdot|s_n) = \pi_{\theta_i}(\cdot|s_n)$适用于contionous problems，像机器人运动；而均匀分布适用于离散任务，如Atari游戏。
对于$s_n$处的每一个action $a_{n,k}$，从$s_n$和$a_{n,k}$处进行rollout，估计$\hat{Q}_{\theta_i}(s_n, a_{n,k})$。在小的有限action spaces情况下，我们可以对从给定状态任何可能的action生成一个rollout，单个$s_n$对$L_{\theta_{old}}$的贡献如下：
$$L_n(\theta) = \sum_{k=1}^K \pi_{\theta} (a_k|s_n) \hat{Q}(s_n, a_k)\tag{28}$$
其中action space是$\mathcal{A} = {a_1, a_2,\cdots, a_K}$。在大的连续state space中，可以使用importance sampling构建一个新的目标近似。从$s_n$处计算的$L_{\theta_{old}}$的self-normalized 估计是：
$$L_n(\theta) = \frac{\sum_{k=1}^K \frac{\pi_{\theta}(a_{n,k}|s_n)}{\pi_{\theta_{old}}(a_{n,k}|s_n)}\hat{Q}(s_n, a_{n,k})}{\sum_{k=1}^K \frac{\pi_{\theta}(a_{n,k}|s_n)}{\pi_{\theta_{old}}(a_{n,k}|s_n)}}\tag{29}$$
假设在$s_n$处执行了$K$个actions $a_{n,1}, a_{n,2}, \cdots, a_{n,K}$。Self-normalized 估计去掉了$Q$值baseline的需要。在$s_n\sim \rho(\pi)$上做平均，可以得到$L_{\theta_{old}}$和它的gradient的估计。
Vine比single path好的地方在于，给定相同数量的$Q$样本，目标函数的局部估计有更低的方差，也就是vine能更好的估计advantage。Vine的缺点在于，需要执行更多steps的模拟计算相应的advantage。此外，vine方法需要对rollout set 中的每一个state都生成多个trajectories，这就需要整个system可以重置到任意的一个state，而single path算法不需要，可以直接应用在真实的system中。

实用算法

使用上面介绍的single path或者vine进行采样，给出两个算法。重复执行以下步骤：

使用single path或者vine算法产生一系列state-action pairs，使用Monte Carlo估计相应的$Q$值；
利用样本计算公式$(27)$中目标函数和约束函数的估计值
使用共轭梯度和line search求出有约束优化问题的近似解，更新policy参数$\theta$，。

在第$3$步中，使用KL散度的Hessian矩阵而不是协方差矩阵的梯度计算Fisher information matrix，即使用$\frac{1}{N}\sum_{n=1}^N \frac{\partial^2}{\partial \theta_j}D_{KL}(\pi_{\theta_{old}}(\cdot|s_n)||\pi_{\theta}(\cdot|s_n))$近似$A_{ij}$而不是$\frac{1}{N}\sum_{n=1}^N \frac{\partial}{\partial \theta_i}log(\pi_{\theta}(a_n|s_n))\frac{\partial}{\partial \partial_j}log(\pi_{\theta}(a_n|s_n))$。
这个实用算法和前面的理论关联如下：

验证了优化使用KL散度进行约束的目标函数可以保证policy improvement是单调递增的。如果penalty系数$C$很大step会很小，我们想要减小这个系数。经验上来讲，很难选择一个鲁邦的penalty系数，所以我们使用一个KL散度上的一个hard constraint而不是一个penalty。
$D_{KL}^{max}(\theta_{old}, \theta)$是很难计算和估计的，所以将约束条件改成对期望$\bar{D}_{KL}(\theta_{old}, \theta)$进行约束。
本文的理论忽略了advantage function的近似误差。

和policy gradient以及natural policy gradient的对比

Policy gradient和natural policy gradient可以看成特殊的trpo，它们可以统一在policy update框架下。The natural policy gradient可以看成公式$(24)$的一个特例：使用$L$的一个linear approximation，和$\bar{D}_{KL}$的一个二次估计，就变成了下面的优化问题：
$$\max_{\theta} \left[\nabla_{\theta}L_{\theta_{old}}(\theta)|_{\theta=\theta_{old}}\cdot (\theta-\theta_{old}) \right]$$
$$s.t. \frac{1}{2}(\theta_{old}-\theta)^T A(\theta_{old})(\theta_{old} - \theta)\le\delta\tag{30}$$
其中$A(\theta_{old})_{ij} = \frac{\partial}{\partial\theta_i}\frac{\partial}{\partial \theta_j}\mathbb{E}_{s\sim \rho_{\pi}}\left[D_{KL}(\pi(\cdot|s, \theta_{old})||\pi(\cdot|s, \theta))\right]_{\theta=\theta_{old}}$，更新公式是$\theta_{new} = \theta_{old}+\frac{1}{\lambda}A(\theta_{old})^{-1} \nabla_{\theta}L(\theta)|_{\theta=\theta_{old}}$，其中步长$\frac{1}{\lambda}$可以看成算法参数。这和trpo不同，在每一次更新都有constraint。尽管这个差别很小，实验表明它能改善在更大规模问题上算法的性能。
同样，也可以使用$l2$约束，推导出标准的policy gradient如下：
$$\max_{\theta} \left[\nabla_{\theta} L_{\theta_{old}}(\theta)|_{\theta=\theta_{old}}\cdot (\theta - \theta_{old})\right] $$
$$s.t. \frac{1}{2}\vert \theta-\theta_{old}\vert^2 \le \delta\tag{31}$$

TRPO算法

TRPO应用了conjugate gradient方法到natural policy gradient，此外，natural policy gradient的trusted region很小，作者将它换成了一个更大的可以调节的值。二次近似可能会降低accuracy，这些可能会对policy的更新引入其他问题，造成performance的degrade。一种可能的解决办法是在进行更新之前先进行验证：

新的policy和老的policy之间的的$\text{KL}$散度是不是小于$\delta$
$L(\theta) \ge 0$

如果验证失败了，使用衰减因子$0\lt \alpha \lt 1$，减小natural policy gradient直到满足要求即可。下面的算法介绍了这种思想的line search solution：
算法 Line Search for TRPO
计算$\Delta_k = \alpha \hat{\text{F}}_k^{-1} \nabla\eta$
for $j=0,1,2,\cdots, t$ do
$\qquad$计算$\theta = \theta_k + \alpha^j \Delta_k$
$\qquad$If $L_{\theta_k}(\theta) \ge 0$或者$\bar{D}_{KL}(\theta||\theta_k) \le \delta$ then
$\qquad\qquad$接受这个更新， $\theta_{k+1} = \theta_k + \alpha^j \Delta_k$
$\qquad\qquad$break
$\qquad$end if
end for
TRPO将truncated natural policiy gradient(使用conjugate gradient)和line search结合起来：
算法 Trust Region Policy Optimization
输入：初始的policy参数$\theta_0$
for $k=0,1,2,\cdots$ do
$\qquad$使用policy $\pi_k = \pi(\theta_k)$收集trajectories到集合$\mathbb{D}_k$
$\qquad$估计优势函数$\hat{A}_t^{\pi_k}$
$\qquad$计算样本估计：
$\qquad\qquad$使用优势函数估计policy gradient $\nabla \eta(\theta)$
$\qquad\qquad$计算$\text{KL}$散度的海塞矩阵（fisher informaction matrix）$\text{H}$
$\qquad$使用共轭梯度算法计算$\hat{\nabla}\eta(\theta) \approx \text{H}^{-1} \nabla\eta(\theta)$
$\qquad$更新$\theta_{k+1} = \theta_k + \alpha \hat{\nabla}\eta(\theta)$
end for

TRPO的缺点

TRPO通过最小化二次泛函近似$\text{F}$的逆，很大程度减少了计算量。但是每一次更新参数还需要计算$\text{F}$。TRPO和其他policy gradient方法相比，采样效率很低，并且扩展性不好，对于很深的网络不适用，这就有了后来的PPO和ACKTR。

Minorize-Maximization MM算法

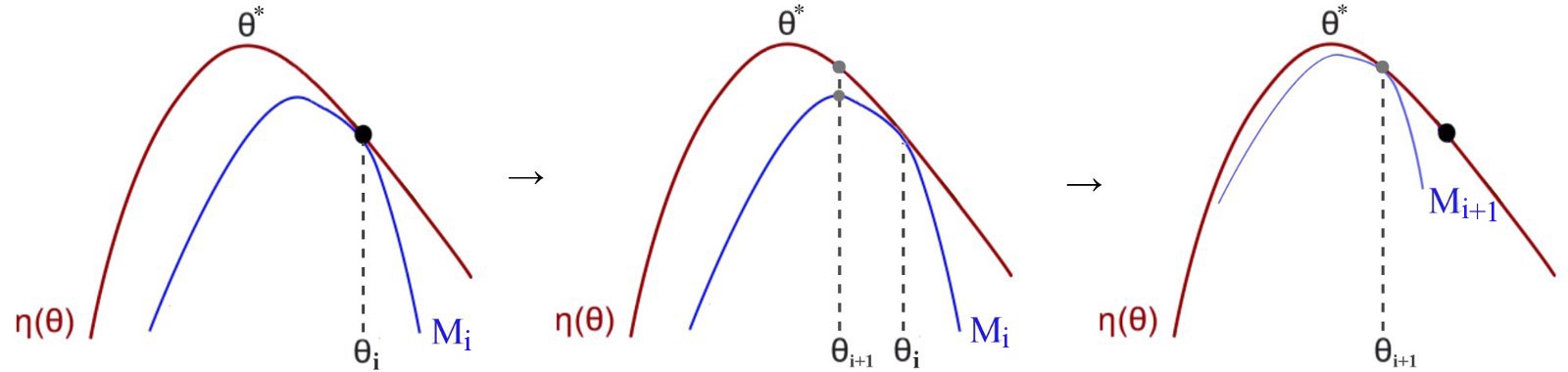
如上图所示，通过迭代的最大化下界函数局部地逼近expected reward。更详细的来说，随机的初始化$\theta$，在当前$\theta$下，找到下界$M$最接近expected reward $\eta$的点，然后将$M$的最优点作为下一次的$\theta$。不断的迭代，直到收敛到optimal policy。这样做有一个条件，就是$M$要比$\eta$容易优化。比如$M$是二次函数：
$$ax^2 + bx+c\tag{32}$$
用向量形式表示是：
$$g\cdot(\theta- \theta_{old}) - \frac{\beta}{2} (\theta- \theta_{old})^T F(\theta - \theta_{old})\tag{33}$$
是一个convex function。
为什么MM算法会收敛到optimal policy，如果$M$是下界的话，它不会跨过红线$\eta$。假设新的$\eta$中的new policy更低，那么blue线一定会越过$\eta$，和$M$是下界冲突。

Trust Region

有两种优化方法：line search和trust region。Gradient descent是line search方法。首先确定下降的方向，然后超这个方向移动一步。而trust region中，首先确定我们想要探索的step size，然后直到在trust region中的optimal point。用$\delta$表示初始的maximum step size，作为trust region的半径：
$$max_{s\in \mathbb{R}^n} m_k(s), \qquad s.t. \vert s\vert \le \delta\tag{34}$$
$m$是原始目标函数$f$的近似，我们的目标是找到半径$\delta$范围$m$的最优点，迭代下去直到最高点。在运行时可以根据表面的曲率延伸或者压缩$\delta$控制学习的速度。如果在optimal point，$m$是$f$的一个poor approximator，收缩trust region。如果approximatation很好，就expand trust region。如果policy改变太多的话，可以收缩trust region。

参考文献

Trust Region Policy Optimization
1.http://joschu.net/docs/thesis.pdf
2.https://arxiv.org/pdf/1502.05477.pdf
3.https://medium.com/@jonathan_hui/rl-trust-region-policy-optimization-trpo-explained-a6ee04eeeee9
4.https://medium.com/@jonathan_hui/rl-trust-region-policy-optimization-trpo-part-2-f51e3b2e373a
5.https://people.eecs.berkeley.edu/~pabbeel/cs287-fa09/readings/KakadeLangford-icml2002.pdf
6.https://drive.google.com/file/d/0BxXI_RttTZAhMVhsNk5VSXU0U3c/view
7.https://zhuanlan.zhihu.com/p/26308073
8.https://zhuanlan.zhihu.com/p/60257706
9.http://rll.berkeley.edu/deeprlcourse/docs/lec5.pdf
10.https://www.zhihu.com/question/316004388