概述
Monte Carlo方法在很多地方都出现过,但是它具体到底是干什么的,之前从来没有仔细了解过,这次正好趁着这个机会好好学习一下。
统计模拟中有一个重要的问题就是给定一个概率分布$p(x)$,生成它的样本。对于一些简单的分布,可以使用均匀分布产生的样本进行样本。但是对于一些复杂的样本,单单使用均匀分布就不行了,需要使用更加复杂的随机模拟方法。Markov Chain Monte Carlo就是一种随机模拟方法(simple simulation),我们常见的gibbs sampling也是。通过多次模拟,产生多组实验数据,进行积分啊什么的。
Monte Carlov Markov Chain
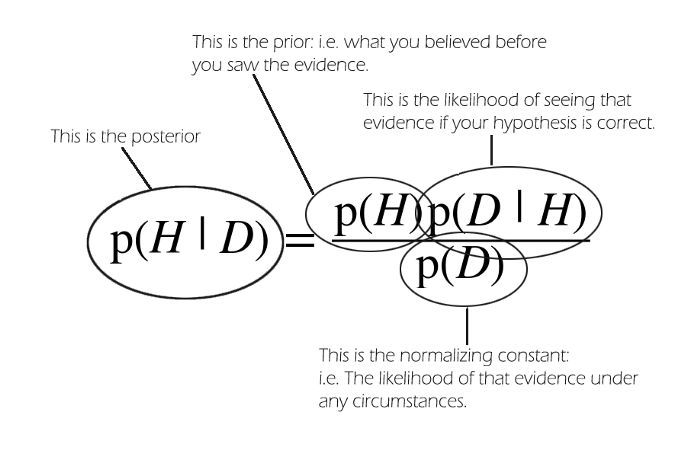
考虑以下,给定一个beta分布,如何进行采样?MCMC提供了从任意概率分布中采样的方法,尤其是当我们计算后验概率时极为有用。在贝叶斯公式中,如下图所示,我们需要从后验分布中进行采样,但是后验分布并不是那么好计算的,因为牵扯到$p(D)$的计算,根据全概率公式,需要进行积分,而beta分布的积分并不好解。
Wikipedia上MCMC的定义:MCMC是一类方法的统称,MCMC方法构建一个Markov chain,这个Markov chain的stationary distribution是我们的目标distribution,然后进行采样。经过很多步之后的一个state可以看成是我们目标distribution的一个样本。简单解释以下就是,给定一个概率分布$p(x)$,我们想要生成这个概率分布的一些样本。因为马尔科夫链能够收敛到stationary distribution,我们的想法就是构造一个转移矩阵为$P$的马尔科夫连,使得该马尔科夫的stationry distribution是$p(x)$,那么不管我们从任何初始状态$x_0$出发,得到一个马尔科夫链$x_0,x_1,\cdots, x_t,x_{t+1}, \cdots$,如果马尔科夫链在第$n$步已经到了stationary distribution,那么$t+1$后的states都可以看成$p(x)$的样本。
示例
我们从Beta分布中进行采样,Beta分布的公式如下所示:
$$f(\theta;\alpha, \beta) = \frac{1}{B(\alpha, \beta)}\theta^{\alpha-1}(1-\theta)^{\beta-1},\alpha\gt 0,\beta\gt 0, x\in \left[0,1\right]$$
其中,$\frac{1}{B(\alpha, \beta)} = \frac{\Gamma(\alpha+\beta)}{\Gamma(\alpha)\Gamma(\beta)}$,是$\alpha,\beta$的函数,这里我们假设$\alpha,\beta$是固定的。
MCMC方法能够创建一个Markov chain,它的stationary distribution是Beta distribution。
定义$s=(s_1,s_2,\cdots, s_M)$是desired stationary distribution。我们的目标是创建一个Markov Chain,它的stationary distribution是desitred stationary distribution。随机初始化一个具有$M$个states的Markov Chain,transition matrix 是$P$,$p_{ij}$代表从state $i$到$j$的概率。
随机初始化的Markov Chain肯定有一个stationary distribution,但是不是我们想要的哪个。我们的目标就是改变这个Markov Chain让它的stationary distribution是我们想要的。为了实现这个目的:
- 随机选择一个初始state $i$
- 根据$P$的第$i$行随机选择一个新的proposal state
- 计算一个measure称作Acceptance Probabiliby:
$$a_{ij} = min(\frac{s_j p_{ji}}{s_ip_{ij}},1)$$ - 投掷一枚正面向上概率为$a_{ij}$的硬币,如果正面向上,accept这个proposal,移动到下一个state,否则,reject 这个proposal,留在当前state。
- 重复下去
经过很长时间以后,这个chain会收敛,我们可以使用这个chain的states作为从任意distribution的采样。不同的分布,使用的acceptance probability不同而已,其实就是根据给出的分布计算一个接收概率而已。
从beta分布中采样
Beta分布是定义在$[0,1]$上的连续分布,它有$[0,1]$上的无穷多个states。假设具有$[0,1]$上无限个states的markov chain的transition matrix $P$是一个对称矩阵,即$p_{ij}=p_{ji}$,acceptance probability中的$p_{ij}$项就可以消掉。
接下来我们要做的是:
- 从均匀分布$(0,1)$中随机选择一个初始state $i$
- 根据$P$的第$i$行值随机选择一个新的proposal state。
- 计算Acceptance Probability:
$$a_{ij} = min(\frac{s_j p_{ji}}{s_ip_{ij}},1)$$
可以化简为:
$$a_{ij} = min(\frac{s_j}{s_i},1)$$
其中$s_i = Ci^{\alpha-1} (1-i)^{\beta-1},s_j = Cj^{\alpha-1} (1-j)^{\beta-1}$, - 投掷一枚正面向上概率为$a_{ij}$的硬币,如果正面向上,accept这个proposal,移动到下一个state,否则,reject 这个proposal,留在当前state。
- 重复下去
参考文献
1.https://stats.stackexchange.com/questions/165/how-would-you-explain-markov-chain-monte-carlo-mcmc-to-a-layperson
2.https://towardsdatascience.com/mcmc-intuition-for-everyone-5ae79fff22b1
3.http://bloglxm.oss-cn-beijing.aliyuncs.com/lda-LDA数学八卦.pdf
4.https://jeremykun.com/2015/04/06/markov-chain-monte-carlo-without-all-the-bullshit/