Markov Matrices
定义
马尔科夫矩阵满足两个条件
- 所有元素大于$0$
- 行向量之和为$1$
属性
- $\lambda = 1$是一个特征值,对应的特征向量的所有分量大于等于$0$。可以直接验证,假设$A = \begin{bmatrix}a&b\\c&d\\ \end{bmatrix}, a + b = 1, c + d = 1$,$A-\lambda I = \begin{bmatrix}a - 1&b\\c&d - 1\\ \end{bmatrix}$,所有元素加起来等于$0$,即$(A-I)\begin{bmatrix}1\\ \vdots\\ 1\end{bmatrix} = 0$,所以这些向量线性相关,因为存在一组不全为$0$的系数使得他们的和为$0$。所以$A-I$是奇异矩阵,也就是说$1$是$A$的一个特征值。
- 所有其他的特征值小于$1$。
Markov Property
简单的来说,就是下一时刻的状态只取决于当前状态,跟之前所有时刻的状态无关,即:
$$P(X_{t+1} = k |X_t=k_t,\cdots, X_1 = k_1) = P(X_{t+1}=k |X_t=k_t) \tag{1}$$
Markov Chain(Process)
如果一个Chain(process)是Markov的,就叫它Markov Chain(Process)。
Stationary Distribution
为什么要用Markov Chain呢?因为它有一个很好的性质,叫做stationary distribution。简单的来说,就是不论初始状态是什么,经过很多步之后,都会达到一个stable state。举个例子,股票有牛市和熊市,还有波动状态,它们的转换关系如下所示:
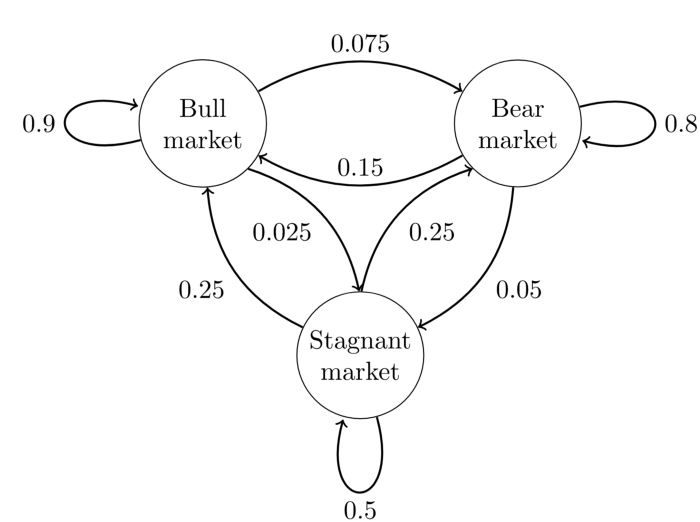
状态转义矩阵矩阵如下表所示:
| 牛市 | 熊市 | 波动 | |
|---|---|---|---|
| 牛市 | 0.9 | 0.075 | 0.025 |
| 熊市 | 0.15 | 0.8 | 0.05 |
| 波动 | 0.25 | 0.25 | 0.5 |
假如从熊市开始,初始state是熊市,用数值表示就是$(0, 1, 0)^T$。根据当前时刻计算下一时刻的公式为:
$$s_{t+1} = s_t Q \tag{2}$$
相应结果为$s_{t+1} = (0.15, 0.8, 0.05)^T$
$t+2$时刻的计算公式为:
$$s_{t+2} = s_t Q^2 \tag{3}$$
这样一直计算下去,可以到达一个稳定state $s$满足:
$$sQ = s \tag{4}$$
对于这个例子来说,不管从什么初始状态开始,最后都会到达稳定状态$s = (0.625, 0.3125, 0.0625)^T$。
那么这个stationary distribution有什么用呢?它能够给出一个process稳定以后在任意时刻某个state出现的概率,比如牛市出现的概率是$62.5\% $,熊市出现的概率是$31.25\%$。
马尔科夫链的稳定性
如果一个非周期性马尔科夫链有转移矩阵$P$,并且它的任意两个状态都是连通的,那么$lim_{n\rightarrow \infty} P_{ij}^m$存在,且与$i$无关,记为$lim_{n\rightarrow \infty }P_{ij}^n = \pi(j)$,即矩阵$P^n$的所有第$j$列都是$\pi(j)$,与$P$的初始值无关。
马尔科夫矩阵的幂
$u_{k+1}=Au_k$,其中$A$是马尔科夫矩阵。我们能得到
$$u_k = A^k u_0 = c_1 \lambda_1^k x_1 + c_2 \lambda_2^k x_2 + \cdots \tag{5}$$
如果只有一个特征值为$1$,对于所有其他特征值$\lambda \neq 1$,当$k\rightarrow \infty$时,幂运算$\lambda^k \rightarrow 0$,能到达一个稳态。
参考文献
1.https://towardsdatascience.com/mcmc-intuition-for-everyone-5ae79fff22b1