TD Learning
TD方法是DP和MC方法的结合,像MC一样,TD可以不需要model直接从experience中学习,像DP一样,TD是bootstrap的方法。
本章的结构和之前一样,首先研究policy evaluation或者叫prediction问题,即给定一个policy $\pi$,估计$v_{\pi}$;然后研究control问题。DP,TD,MC方法都是使用GPI方法解control问题,不同点在于prediction问题的解法。
为什么叫TD?
因为TD更新是基于不同时间上两个estimate的估计进行的。
TD prediction
TD和MC都是利用采样获得的experience求解prediction问题。给定policy $\pi$下的一个experience,TD和MC方法使用该experience中出现的non-terminal state $S_t$估计$v_{\pi}$的$V$。他们的不同之处在于MC需要等到整个experience的return知道以后,把这个return当做$V(S_t)$的target,every visit MC方法的更新规则如下:
$$V(S_t) = V(S_t) + \alpha \left[G_t - V(S_t)\right]\tag{1}$$
其中$G_t$是从时刻$t$到这个episode结束的return,$\alpha$是一个常数的步长,这个方法叫做$constant-\alpha$ MC。MC方法必须等到一个episode结束,才能进行更新,因为只有这个时候$G_t$才知道。为了更方便的训练,就有了TD方法。TD方法做的改进是使用$t+1$时刻state $V(S_{t+1})$的估计值和reward $R_{t+1}$的和作为target:
$$V(S_t) = V(S_t) + \alpha \left[R_{t+1}+\gamma V(S_{t+1}) - V(S_t)\right]\tag{2}$$
如果V在变的话,是不是应该是下面的公式??
$$V_{t+1}(S_t) = V_t(S_t) + \alpha \left[R_{t+1}+\gamma V_t(S_{t+1}) - V_t(S_t)\right]$$
即只要有了到$S_{t+1}$的transition并且接收到了reward $R_{t+1}$就可以进行上述更新。MC方法的target是$G_t$,而TD方法的target是$\gamma V(S_{t+1} + R_{t+1})$,这种TD方法叫做$TD-0$或者$one\ step\ TD$,它是$TD(\lambda)$和$n-step\ TD$的一种特殊情况。
算法
下面是$TD(0)$的完整算法:
算法1 Tabular TD(0) for $V$
输入: 待评估的policy $\pi$
算法参数:步长$\alpha \in (0,1]$
初始化: $V(s), \forall s\in S^{+},V(terminal) = 0$
Loop for each episode
$\qquad$初始化$S$
$\qquad A\leftarrow \pi(a|S)$
$\qquad$Loop for each step of episode
$\qquad\qquad$执行action $A$,得到$S’$和$R$
$\qquad\qquad V(S) = V(S) + \alpha \left[R + \gamma V(S’) - V(S)\right]$
$\qquad\qquad$$S\leftarrow S’$
$\qquad$Until $S$ 是terminal state
$TD(0)$是bootstrap方法,因为它基于其他state的估计value进行更新。从第三章中我们知道:
\begin{align*}
v_{\pi}(s) & = \mathbb{E}_{\pi}\left[G_t\right]\tag{3}\\
& = \mathbb{E}_{\pi}\left[R_{t+1}+\gamma G_{t+1}| S_t = s\right]\tag{4}\\
& = \mathbb{E}_{\pi}\left[R_{t+1}+\gamma v_{\pi}(S_{t+1})|S_t = s\right]\tag{5}\\
\end{align*}
MC使用式子$(3)$的estimate作为target,而DP使用式子$(5)$的estimate作为target。MC方法用一个sample的return代替式子$(3)$中真实的未知expected return $G_t$;DP是用$V(S_{t+1})$作为$v_{\pi}(S_{t+1})$的一个估计,因为$v_{\pi}(S_{t+1})$的真实值是不知道的。TD结合了MC的采样以及DP的bootstrap,它对式子$(4)$的tranisition进行sample,同时使用$v_{\pi}$的估计值$V$进行计算。

TD的backup图如图所示。TD和MC updates被称为sample updates,因为这两个算法的更新都牵涉到采样一个sample successor state,使用这个state的value和它后继的这条路上的reward计算一个backed-up value,然后根据这个值更新该state的value。sample updates和DP之类的expected updates的不同在于,sample updates使用一个sample successor进行更新,expected updates使用所有可能的successors distribution进行更新。
$R_{t+1} + \gamma V(S_{t+1}) - V(S_t)$可以看成一种error,衡量了$S_t$当前的estimated value $V(S_t)$和一个更好的estimated value之间的差异$R_{t+1} +\gamma V(S_{t+1})$,我们把它叫做$TD-error$,用$\delta_t$表示。$\delta_t$是$t$时刻的$TD-error$,在$t+1$时刻可用,用公式表示是:
$$\delta_t = R_{t+1} + \gamma V(S_{t+1}) - V(S_t) \tag{6}$$
如果$V$在一个episode中改变的话,那么上述公式是不是应该写成:
$$\delta_t = R_{t+1} + \gamma V_t(S_{t+1}) - V_t(S_t)$$
应该在$t$时刻,计算的TD error是用来更新$t+1$时刻的value的。如果$V$在一个episdoe中不变的话,就像MC方法一样,那么MC error可以写成TD errors的和。
\begin{align*}
G_t - V(S_t) & = R_{t+1} + \gamma G_{t+1} - V(S_t) + \gamma V(S_{t+1}) - \gamma V(S_{t+1})\\
& = R_{t+1} + \gamma V(S_{t+1}) - V(S_t) + \gamma G_{t+1} - \gamma V(S_{t+1})\\
& = \delta_t + \gamma G_{t+1} - \gamma V(S_{t+1})\\
& = \delta_t + \gamma(G_{t+1} - V(S_{t+1}))\\
& = \delta_t + \gamma\delta_{t+1} + \gamma^2(G_{t+2} - V(S_{t+2}))\\
& = \delta_t + \gamma\delta_{t+1} + \gamma^2\delta_{t+2} + \cdots + \gamma^{T-t-1}\delta_{T-1} + \gamma^{T-t}(G_T-V(S_T))\\
& = \delta_t + \gamma\delta_{t+1} + \gamma^2\delta_{t+2} + \cdots + \gamma^{T-t-1}\delta_{T-1} + \gamma^{T-t}(0-0)\\
& = \sum_{k=t}^{T-1} \gamma^{k-t}\delta_k \tag{7}\\
\end{align*}
如果$V$在一个episode中改变了的话,像$TD(0)$一样,这个公式就不精确成立了,如果$\alpha$足够小的话,还是近似成立的。
$$\delta_t = R_{t+1} + \gamma V_t(S_{t+1}) - V_t(S_t)$$
\begin{align*}
V_{t+1}(S_t) &= V_t(S_t) + \alpha \left[R_{t+1}+\gamma V_t(S_{t+1}) - V_t(S_t)\right]\\
&= V_t(S_t) + \alpha \delta_t
\end{align*}
\begin{align*}
G_t - V_t(S_t) & = R_{t+1} + \gamma G_{t+1} - V_t(S_t) + \gamma V_{t+1}(S_{t}) - \gamma V_{t+1}(S_{t})\\
& = R_{t+1} + \gamma V_{t+1}(S_{t}) - V_t(S_t) + \gamma G_{t+1}- \gamma V_{t+1}(S_{t})\\
& = R_{t+1} + \gamma (V_t(S_t) + \alpha \delta_t) - V_t(S_t) + \gamma G_{t+1}- \gamma V_{t+1}(S_{t})\\
& = R_{t+1} + \gamma V_t(S_t) - V_t(S_t) + \gamma \alpha \delta_t + \gamma G_{t+1}- \gamma V_{t+1}(S_{t})\\
\end{align*}
然而上面是错误的,因为$\delta_t$需要的是$V_t(S_{t+1})$
\begin{align*}
G_t - V_t(S_t) & = R_{t+1} + \gamma G_{t+1} - V_t(S_t) + \gamma V_{t+1}(S_{t+1}) - \gamma V_{t+1}(S_{t+1})\\
& = R_{t+1} + \gamma V_{t+1}(S_{t+1}) - V_t(S_t) + \gamma G_{t+1}- \gamma V_{t+1}(S_{t+1})\\
\end{align*}
\begin{align*}
\delta_t &= R_{t+1} + \gamma V_t(S_{t+1}) - V_t(S_t)\\
\delta_{t+1} &= R_{t+2} + \gamma V_{t+1}(S_{t+2}) - V_{t+1}(S_{t+1})\\
\delta_{t+2} &= R_{t+3} + \gamma V_{t+2}(S_{t+3}) - V_{t+2}(S_{t+2})\\
\delta_{t+3} &= R_{t+4} + \gamma V_{t+3}(S_{t+4}) - V_{t+3}(S_{t+3})\\
\end{align*}
\begin{align*}
&\delta_t+\delta_{t+1}+\delta_{t+2}+\delta_{t+3}\\
= &R_{t+1} + \gamma V_t(S_{t+1}) - V_t(S_t)\\
+&R_{t+2} + \gamma V_{t+1}(S_{t+2}) - V_{t+1}(S_{t+1})\\
+&R_{t+3} + \gamma V_{t+2}(S_{t+3}) - V_{t+2}(S_{t+2})\\
+&R_{t+4} + \gamma V_{t+3}(S_{t+4}) - V_{t+3}(S_{t+3})\\
\end{align*}
OK。。。还是没有算出来。。
TD例子
TD的一个例子。每天下班的时候,你会估计需要多久能到家。你回家的事件和星期,天气等相关。在周五的晚上6点,下班之后,你估计需要30分钟到家。到车旁边是$6:05$,而且天快下雨了。下雨的时候会有些堵车,所以估计从现在开始大概还需要$35$分钟才能到家。十五分钟后,下了高速,这个时候你估计总共的时间是$35$分钟(包括到达车里的$5$分钟)。然后就遇到了堵车,真正到达家里的街道是$6:40$,三分钟后到家了。
| State | Elapsed Time | Predicted Time to Go | Predicted Total Time |
|---|---|---|---|
| leaveing office | 0 | 30 | 30 |
| reach car | 5 | 35 | 40 |
| 下高速 | 20 | 15 | 35 |
| 堵车 | 30 | 10 | 40 |
| 门口的街道 | 40 | 3 | 43 |
| 到家 | 43 | 0 | 43 |
rewards是每一个journey leg的elapsed times,这里我们研究的是evaluation问题,所以可以直接使用elapsed time,如果是control问题,要在elapsed times前加负号。state value是expected time。上面的第一列数值是reward,第二列是当前state的value估计值。
如果使用$\alpha = 1$的TD和MC方法。对于MC方法,对于$S_t$的所有state,都有:
\begin{align*}
V(S_t) &= V(S_t) + (G_t - V(S_t))\\
& = G_t \\
& = 43
\end{align*}
对于TD方法,让$\gamma=1$,有:
\begin{align*}
V(S_t) &= V_t(S_t) + \alpha (R_{t+1} + \gamma V_t(S_{t+1}) - V(S_t))\\
&= R_{t+1} + V_t(S_{t+1})
\end{align*}
TD Prediction的好处
TD是bootstrap方法,相对于MC和DP来说,TD的好处有以下几个:
- 相对于DP,不需要environment, reward model以及next-state probability distribution。
- 相对于MC,TD是online,incremental的。MC需要等到一个episode结束,而TD只需要等一个时间步(本节介绍的TD0)。
- TD在table-base case可以为证明收敛,而general linear function不一定收敛。
但是具体TD好还是MC好,目前还没有明确的数学上的理论证明。而实践上表明,TD往往要比constant $\alpha$ MC算法收敛的快。
TD(0)的优势
如果我们只有很少的experience的话,比如有$10$个episodes,或者有$100$个timesteps。这种情况下,我们会重复的使用这些这些experience进行训练直到算法收敛。具体方法是,给定一个approximate value function $V$,在每一个只要不是terminal state的时间$t$处,计算MC和TD增量,最后使用所有增量之和只更新value function一次。举个例子好了,假如我们有三个episdoes,
A,B,C
B,A
A,A
更新的方法是,$V(A) = V(A) + \alpha(G_1 - V(A) + G_2 - V(A) + G_{31} - V(A) + G_{32} -V(A))$
这种方法叫做batch updating,因为只有在一个batch完全处理完之后才进行更新,其实这个和DP挺像的,只不过DP直接利用的是environment dynamic,而我们使用的是样本。
在batch updating中,TD(0)一定会收敛到一个与$\alpha$无关的结果,只要$\alpha$足够下即可,同理batch constant $\alpha$ MC算法同样条件下也会收敛到一个确定的结果,只不过和batch TD结果不同而已。Normal updating的方法并没有朝着整个batch increments的方法移动,但是大概方向差不多。其实就是一个把整个batch的所有experience的increment加起来一起更新,一个是每一个experience更新一次,就这么点区别。
具体来说,batch TD和batch MC哪个更好一些呢?这就牵扯到他们的原理了。Batch MC的目标是最小化training set上的mse,而batch TD的目标是寻找Markov process的最大似然估计。一般来说,maximum likeliood estimate是进行参数估计的。在这里的话,TD使用mle从已有episodes中生成markov process模型的参数:从$i$到$j$的transition probatility是观测到从$i$到$j$的transition所占的百分比,对应的expected reward是观测到的rewards的均值。给出了这个model之后,如果这个模型是exactly correct的话,那么我们就可以准确的计算出value function的estimate,这个成为certainty-equivalence estimate,因为它相当于假设markov process的model是一致的,而不是approximated,一般来说,batch TD(0)收敛到cetainty-equivalence estimate。
从而,我们可以简单的解释以下为什么batch TD比batch MC收敛的快。因为batch TD计算的是真实的cetainty-equivalence estimate。同样的,对于non batch的TD和MC来说,虽然TD没有使用cetainty-equivalence,但是它们大概在向那个方向移动。
尽管cetrinty-equivalence是最优解,但是,但是,但是,cost太大了,如果有$n$个states,计算mle需要$n^2$的空间,计算value function时候,需要$n^3$的计算步数。当states太多的话,实际上并不可行,还是老老实实的使用TD把,只会用不超过$n$的空间。。
TD具体算法介绍
Sarsa
介绍
Sarsa是一个on-policy的 TD control算法。按照GPI的思路来,先进行policy evaluation,在进行policy improvement。首先解prediction问题,按照以下action value的$TD(0)$公式估计当前policy $\pi$下,所有action和state的$q$值$q_{\pi}(s,a)$:
$$Q(S_t,A_T) \leftarrow Q(S_t,A_t) + \alpha \left[R_{t+1} + \gamma Q(S_{t+1}, A_{t+1}) -Q(S_t,A_t)\right] \tag{8}$$
当$S_{t+1} = 0$时,$Q(S_{t+1}, A_{t+1})=0$,相应的backup diagram如下图所示。

第二步解control问题,在on-policy的算法中,不断的估计behaviour policy $\pi$的$q_{\pi}$,同时改变$\pi$朝着$q_{\pi}$更大的方向移动。Sarsa算法中,behaviour policy和target policy是一样的,在不断的改变。完整的算法如下:
Sarsa算法(on-policy control) 估计$Q\approx q_$*
对于所有$s\in S^{+}, a\in A(s)$,随机初始化$Q(s,a)$,$Q(terminal, \cdot) = 0$
Loop for each episode
$\qquad$ 获得初始状态$S$
$\qquad$ 使用policy(如$\epsilon$-greedy算法)根据state $S$选择当前动作$A$
$\qquad$ Loop for each step of episode
$\qquad\qquad$ 采取action,得到R和S’
$\qquad\qquad$ 使用policy(和上面的policy一样)根据S’选择A’
$\qquad\qquad Q(S,A) \leftarrow Q(S,A) + \alpha \left[R+ \gamma Q(S’,A’) - Q(S,A)\right]$
$\qquad\qquad S\leftarrow S’, A\leftarrow A’$
$\qquad$ until $S$是terminal
示例
Q-learning
$$Q(S_t,A_T) \leftarrow Q(S_t,A_t) + \alpha \left[R_{t+1} + \gamma max Q(S_{t+1}, A_{t+1}) -Q(S_t,A_t)\right]\tag{9}$$
这一节介绍的是off-policy的TD contrl算法,Q-learning。对于off-policy算法来说,behaviour policy用来选择action,target policy是要评估的算法。在Q-learning算法中,直接学习的就是target policy的optimal action value function $q_{*}$,和behaviour policy无关。完整的Q-learning算法如下:
Q-learning算法(off-policy control) 估计$\pi \approx \pi_{*}$
对于所有$s\in S^{+}, a\in A(s)$,随机初始化$Q(s,a)$,$Q(terminal, \cdot) = 0$
Loop for each episode
$\qquad$ 获得初始状态$S$
$\qquad$ Loop for each step of episode
$\qquad\qquad$ 使用behaviour policy(如$\epsilon$-greedy算法)根据state $S$选择当前动作$A$
$\qquad\qquad$ 执行action $A$,得到$R$和$S’$
$\qquad\qquad Q(S,A) \leftarrow Q(S,A) + \alpha \left[R+ \gamma max Q(S’,A’) - Q(S,A)\right]$
$\qquad\qquad S\leftarrow S’$
$\qquad$ until $S$是terminal
Expected Sarsa
Q-learning对所有next state-action pairs取了max操作。如果不是取max,而是取期望呢?
\begin{align*}
Q(S_t,A_T) & \leftarrow Q(S_t,A_t) + \alpha \left[R_{t+1} + \gamma \mathbb{E}_{\pi}\left[ Q(S_{t+1}, A_{t+1})| S_{t+1} \right] -Q(S_t,A_t)\right]\\
&\leftarrow Q(S_t,A_t) + \alpha \left[R_{t+1} + \gamma \sum_a\pi(a|S_{t+1})Q -Q(S_t,A_t)\right]\tag{10}
\end{align*}
其他的和Q-learning保持一致。给定next state $S_{t+1}$,算法在expectation上和sarsa移动的方向一样,所以被称为expected sarsa。这个算法可以是on-policy,但是通常它是是off-policy的。比如,on-policy的话,policy使用$\epsilon$ greedy算法,off-policy的话,behaviour policy使用stochastic policy,而target policy使用greedy算法,这其实就是Q-learning算法了。所以,Expected Sarsa实际上是对Q-learning的一个归纳,同时又有对Sarsa的改进。
Q-learning和Expected Sarsa的backup diagram如下所示:

Sarsa vs Q-learning vs Expected Sarsa
Sarsa是on-policy的,behaviour policy和target policy一直在变($\epsilon$在变),但是behaviour policy和target policy一直都是一样的。
Q-learning是off-policy的,target policy和behaviour policy一直都不变(可能$\epsilon$会变,但是这个不是Q-learning的重点),behaviour policy保证exploration,target policy是greedy算法。
Q-learning是off-policy算法,那么又为什么one-step Q-learning不需要importance sampling?Importance sampling的作用是为了使用policy $b$下观察到的rewards估计policy $\pi$下的expected rewards。尽管在Q-learning中,behaviour policy和target policy不同,behaviour policy仅仅用来采样$s_t, a_t, R_{t+1}$,在更新$Q$值时,使用target policy(epsilon policy)生成的实际上是$a’ = \max_a Q(s_{t+1}, a)$。Target policy和behaviour policy不同的实际上是$a_t$,但是在更新$Q$值时,用的也是$a_t$。也就是说使用behaviour policy选择的是$a_t$,接下来使用target policy选择执行$a_t$后的新action $a_{t+1}$。
Q(0)和Expected Sarsa(0)都没有使用importance sampling,因为在$Q(s,a)$中,action $a$已经被选择了,用哪个policy选择的是无关紧要的,TD error可以使用$Q(s’,*)$上的boostrap进行计算,而不需要behaviour policy。
Maximization Bias和Double Learning
目前介绍的所有control算法,都涉及到target polices的maximization操作。Q-learning中有greedy target policy,Sarsa的policy通常是$\epsilon$ greedy,也会牵扯到maximization。Max操作会引入一个问题,加入某一个state,它的许多action对应的$q(s,a)=0$,然后它的估计值$Q(s,a)$是不确定的,可能比$0$大,可能比$0$小,还可能就是$0$。如果使用max $Q(s,a)$的话,得到的值一定是大于等于$0$的,显然有一个positive bias,这就叫做maximization bias。
Maximization Bias例子
给出如下的一个例子:
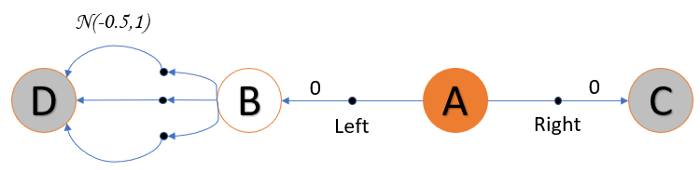
这个MDP有四个state,A,B,C,D,C和D是terminal state,A总是start state,并且有left和right两个action,right action转换到C,reward是0,left action转换到B,reward是$0$,B有很多个actions,都是转换到$D$,但是rewards是不同,reward服从一个均值为$-0.5$,方差为$1.0$的正态分布。所以reward的期望是负的,$-0.5$。这就意味着在大量实验中,reward的均值往往是小于$0$的。
基于这个假设,在A处总是选择left action是很蠢的,但是因为其中有一些reward是positive,如果使用max操作的话,整个policy会倾向于选择left action,这就造成了在一些episodes中,reward是正的,但是如果在long run中,reward的期望就是负的。
Maximizaiton Bias出现的直观解释
那么为什么会出现这种问题呢?
用$X1$和$X2$表示reward的两组样本数据。如下所示:
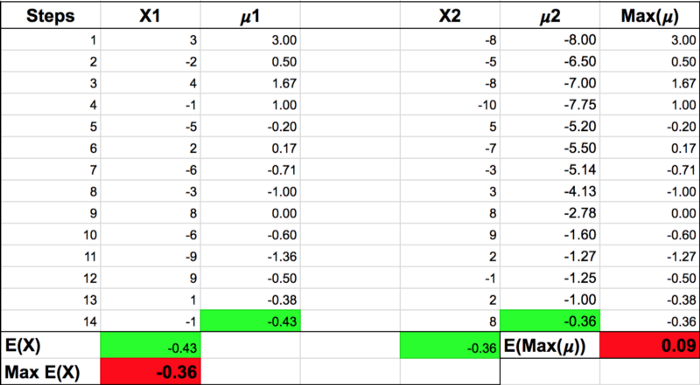
在$X1$这组样本中,样本均值是$-0.43$,X2样本均值是$-0.36$。在增量式计算样本均值$\mu$时,得到的最大样本均值的期望是$0.09$,而实际上计算出来的期望的最大值$\mathbb{E}(X)$是$-0.36$。要使用$\mathbb{E} \left[max\ (\mu)\right]$估计$max\ \mathbb{E}(X)$,显然它们的差距有点大,$max(\mu)$是$max E(X)$的有偏估计。也就是说使用$max Q(s’,a’)$更新$Q(s,a)$时,$Q(s,a)$并没有朝着它的期望$-0.5$移动。估计这只是一个直观的解释,严格的证明可以从论文中找。
如何解决Maximization Bias问题
那么怎么解决这个问题呢,就是同时学习两个$Q$函数$Q_1, Q_2$,这两个$Q$函数的地位是一样的,每次随机选择一个选择action,然后更新另一个。证明的话,Van Hasselt证明了$\mathbb{E}(Q_2(s’,a*)\le max\ Q_1(s’,a*)$,也就是说$Q_1(s,a)$不再使用它自己的max value进行更新了。
下面是$Q$-learning和Double $Q$-learning在训练过程中在A处选择left的统计:
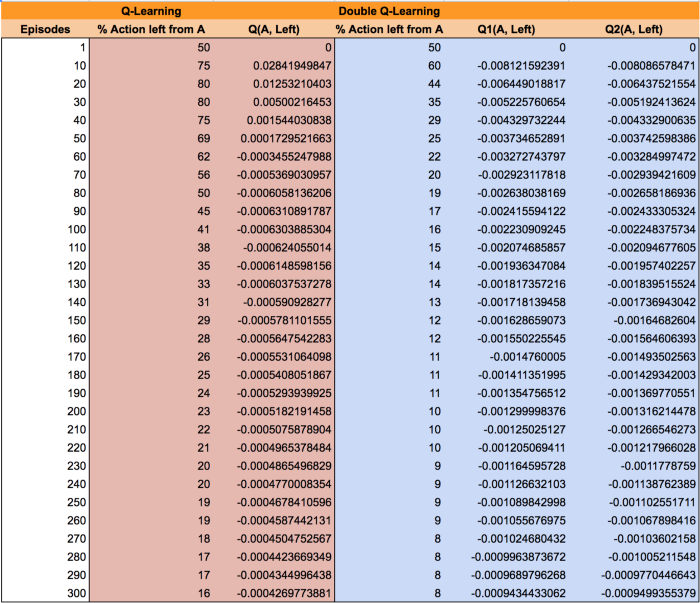
可以看出来,Double $Q$-learning要比$Q$-learning收敛的快和好。
当然,Sarsa和Expected Sarsa也有maximization bias问题,然后有对应的double版本,Double Sarsa和Double Expected Sarsa。
Afterstates
之前介绍了state value function和action value function。这里介绍一个afterstate value function,afterstate value function就是在某个state采取了某个action之后再进行评估,一开始我想这步就是action value function。事实上不是的,action value function估计的是$Q(s,a)$,重点是state和action这些pair,对于afterstate value来说,可能有很多个state和action都能到同一个next state,这个时候它们的作用是一样的,因为我们估计的是next state的value。
象棋就是一个这样的例子。。这里只是介绍一下,还有很多各种各样特殊的形式,它们可以用来解决各种各样的特殊问题。具体可以自己多了解一下。
总结
这一章主要介绍了最简单的一种TD方法,one-step,tabular以及model-free。接下来的两章会介绍一些n-step的TD方法,可以和MC方法联系起来,以及包含一个模型的方法,和DP联系起来。在第二部分的时候,会将tabular的TD扩展到function approximation的形式,和deep learning以及artificial neural networks联系起来。
参考文献
1.《reinforcement learning an introduction》第二版
2.https://stats.stackexchange.com/a/297892
3.https://towardsdatascience.com/double-q-learning-the-easy-way-a924c4085ec3
4.https://stats.stackexchange.com/a/347090/254953