MC Methods
这章主要介绍了MC算法,MC算法通过采样,估计state-value function或者action value function。为了找到最好的policy,需要让policy不断的进行探索,但是我们还需要找到最好的action,减少exploration。这两个要求是矛盾的,这一章主要介绍了两种方法来尽量满足这两个要求。一种是on-policy的方法,使用soft policy,即有一定概率随机选择action,其余情况下选择最好的action。这种情况下学习到的policy不是greedy的,同时也能进行一定的exploration。一种是off-policy的方法,这种方法使用两个不同的policy,一个用来采样的behaviour policy,一个用来评估的target policy。target policy是一个deterministic policy,而behaviour policy用来exploration。
MC方法通过采样估计值函数有三个优势,从真实experience中学习,从仿真环境中学习,以及每个state value的计算独立于其他state。
MC和DP不一样的是,它不需要环境的信息,只需要experience即可,不管是从真实交互还是从仿真环境中得到的state,action,reward序列都行。从真实交互中学习不需要环境的信息,从仿真环境中学习需要一个model,但是这个model只用于生成sample transition,并不需要像DP那样需要所有transition的完整概率分布。在很多情况下,生成experience sample要比显示的得到概率分布容易很多。
MC基于average sample returns估计值函数。为了保证returns是可用的,这里定义蒙特卡洛算法是episodic的,即所有的experience都有一个terminal state。只有在一个episode结束的时候,value estimate和policy才会改变。蒙塔卡洛算法可以在episode和episode实现增量式,不能在step和step之间实现增量式。(Monte Carlo methods can thus be incremental in an episode-by-episode sense, but not in a step-by-step online sense.)
在一个state采取action得到的return取决于同一个episode后续状态的action,因为所有的action都是在不断学习中采取,从早期state的角度来看,这个问题是non-stationary的。为了解决non-stationary问题,采用GPI中的idea。DP从已知的MDP中计算value function,蒙特卡洛使用MDP的sample returns学习value function。然后value function和对应的policy交互获得好的value和policy。
这一章就是把DP中的各种想法推广到了MC上,解决prediction和control问题,DP使用的是整个MDP,而MC使用的是MDP的采样。
MC Prediction
Prediction problem就是估计value function,value function又分为state value function和action value function。这里会分别给出state value function和action value function的估计方法。
State value function
从state value function说起。最简单的想法就是使用experience估计value function,通过对每个state experience中return做个average。
First visti MC method
这里主要介绍两个算法,一个叫做first visit MC method,另一个是every visit MC method。比如要估计策略$\pi$下的$v(s)$,使用策略$\pi$采样一系列经过$s$的episodes,$s$在每一个episode中出现一次叫做一个visit,一个$s$可能在一个episode中出现多次。First visit就是只取第一次visit估计$v(s)$,every visit就是每一次visit都用。
下面给出first visit的算法:
算法1 First visit MC preidction
输入 被评估的policy $\pi$
初始化:
$\qquad V(s)\in R,\forall s \in S$
$\qquad Returns(s) \leftarrow empty list,\forall s \in S$
Loop for each episeode:
$\qquad$生成一个episode
$\qquad G\leftarrow 0$
$\qquad$Loop for each step, $t= T-1,T-2, \cdots, 1$
$\qquad\qquad G\leftarrow G + \gamma R_t$
$\qquad\qquad$ IF $S_t$没有在$S_0, \cdots , S_{t-1}$中出现过
$\qquad\qquad\qquad Returns(S_t).apppend(G)$
$\qquad\qquad\qquad V(S_t)\leftarrow average(Returns(S_t))$
$\qquad\qquad END IF$
Every visit算法的话,不用判断$S_t$是否出现。当$s$的visit趋于无穷的时候,first vist和every visit算法$v_{\pi}(s)$都能收敛。First visit中,每一个return都是$v_{\pi}(s)$的一个独立同分布估计。根据大数定律,估计平均值($average(Returns(S_0),\cdots, average(Returns(S_t)$)的序列收敛于它的期望。每一个average都是它自己的一个无偏估计,标准差是$\frac{1}{\sqrt{n}}$。every visit的收敛更难直观的去理解,但是它二次收敛于$v_{\pi}(s)$。
补充一点:
大数定律:无论抽象分布如何,均值服从正态分布。
中心极限定理:样本大了,抽样分布近似于整体分布。
这里再次对比一下DP和MC,在扑克牌游戏中,我们知道环境的所有信息,但是我们不知道摸到下一张牌的概率,比如我们手里有很多牌了,我们知道下一张摸到什么牌会赢,但是我们不知道这件事发生的概率。使用MC可以采样获得,所以说,即使有时候知道环境信息,MC方法可能也比DP方法好。
MC backup diagram
能不能推广DP中的backup图到MC中?什么是backup图?backup图顶部是一个root节点,表示要被更新的节点,下面是所有的transitions,leaves是对于更新有用的reward或者estimated values。
MC中的backup图,root节点是一个state,下面是一个episode中的所有transtion轨迹,以terminal state为终止节点。DP backup diagram展示了所有可能的transitions,而MC backup diagram只展示了采样的那个episode;DP backup diagram只包含一步的transitions,而MC backup diagram包含一个episode的所有序列。
MC的特点
DP中每个state的估计都依赖于它的后继state,而MC中每个state value的计算都不依赖于任何其他state value(MC算法不进行bootstrap),所以可以单独估计某一个state或者states的一个子集。而且估计单个state的计算复杂度和states的数量无关,我们可以只取感兴趣的states子集进行评估,这是MC的第三个优势。前两个优势是从actural experience中学习和从simulated的experience中学习。
Action value function
如果没有model的话,需要估计state-action value而不是state value。有model的话,只有state value就可以确定policy,选择使reward和next_state value加起来最大的action即可。没有model的话,只有state value是不够的,因为不知道下一个state是什么。而使用action value,就可以确定policy,选择$q$值最大的那个action value,取相应的action即可。
所以这一节的目标是学习action value function。有一个问题是许多state-action可能一次也没有被访问过,如果$\pi$是deterministic的,每一个state只输出一个action,其他action的MC估计没有returns进行平均,就无法进行更新。所以,我们需要估计每一个state对应的所有action,这是exploration问题。
对于action value的policy evaluation,必须保证continual exploration。一种实现方式是指定episode开始的state-action pair,每一个pair都有大于$0$的概率被选中,这就保证了每一个action-pair在无限个episode中会被访问无限次,这叫做exploring starts。这种假设有时候有用,但是在某些时候,我们无法控制环境产生的experience,可行的方法是使用stochastic policy。
MC Control
MC control使用的还是GPI的想法,估计当前policy的action value,基于action value改进policy,不断迭代。考虑经典的policy iteration,执行一次完全的iterative policy evaluation,再执行一次完全的policy improvement,不断迭代。对于policy evaluation,每次evaluation都使用多个episodes的experience,每次action value都会离true value function更近。假设我们有无限个exploring starts生成的episodes,满足这些条件时,对于任意$\pi_k$都会精确计算出$q_{\pi_k}$。进行policy improvement时,只要对于当前的action value function进行贪心即可,即:
$$\pi(s) = arg\ max_a q(s,a)\tag{1}$$
第$4$章给出了证明,即policy improvement theorem。在每一轮improvement中,对所有的$s\in S$,执行:
\begin{align*}
q_{\pi_k}(s,\pi_{k+1}(s)) &=q_{\pi_k}(s, argmax_a q_{\pi_k}(s,a))\\
&=max_a q_{\pi_k}(s,a)\\
&\ge q_{\pi_k}(s, \pi_k(s))\\
&\ge v_{\pi_k}(s)\\
\end{align*}
MC算法的收敛保证需要满足两个假设,一个是exploring start,一个是policy evaluation需要无限个episode的experience。但是现实中,这两个条件是不可能满足的,我们需要替换掉这些条件近似接近最优解。
MC Control without infinte episodes
无限个episodes的条件比较容易去掉,在DP方法中也有这些问题。在DP和MC任务中,都有两种方法去掉无限episode的限制,第一种方法是像iterative policy evaluation一样,规定一个误差的bound,在每一次evaluation迭代,逼近$q_{\pi_k}$,通过足够多的迭代确保误差小于bound,可能需要很多个episode才能达到这个bound。第二种是进行不完全的policy evaluation,和DP一样,使用小粒度的policy evaluation,可以只执行iterative policy evaluation的一次迭代,也可以执行一次单个state的improvement和evaluation。对于MC方法来说,很自然的就想到基于一个episode进行evaluation和improvement。每经历一个episode,执行该episode内相应state的evaluation和improvement。也就是说一个是规定每次迭代的bound,一个是规定每次迭代的次数。
伪代码
算法2 First visit MCES
初始化
$\qquad$任意初始化$\pi(s)\in A(s), \forall s\in S$
$\qquad$任意初始化$Q(s, a)\in R, \forall s\in S, \forall a \in A(s)$
$\qquad$Returns(s,a)$\leftarrow$ empty list, $\forall s\in S, \forall a \in A(s)$
Loop forever(for each episode)
$\qquad$随机选择满足$S_0\in S, A_0\in A(S_0)$的state-action$(S_0,A_0)$,满足概率大于$0$
$\qquad$从$S_0,A_0$生成策略$\pi$下的一个episode,$S_0,A_0,R_1,\cdots,S_{T-1},A_{T-1},R_T$
$\qquad G\leftarrow 0$
$\qquad$Loop for each step of episode,$t=T-1,T-2,\cdots,0$
$\qquad\qquad G\leftarrow \gamma G+R_{t+1}$
$\qquad\qquad$如果$S_t,A_t$没有在$S_0,A_0,\cdots, S_{t-1},A_{t-1}$中出现过
$\qquad\qquad\qquad$Returns($S_t,A_t$).append(G)
$\qquad\qquad\qquad Q(S_t,A_t) \leftarrow average(Returns(S_t, A_t)$
$\qquad\qquad\qquad \pi(S_t) \leftarrow argmax_a Q(S_t,a)$
这个算法一定会收敛到全局最优解,因为如果收敛到一个suboptimal policy,value function在迭代过程中会收敛到该policy的true value function,接下来的policy improvement会改进该suboptimal policy。
On-policy MC Control without ES
上节主要是去掉了无穷个episode的限制,这节需要去掉ES的限制,解决方法是需要agents一直能够去选择所有的actions。目前有两类方法实现,一种是on-policy,一种是off-policy。
on-policy和off-policy
On-policy算法中,用于evaluation或者improvement的policy和用于决策的policy是相同的,而off-policy算法中,evaluation和improvement的policy和决策的policy是不同的。
$\varepsilon$ soft和$\varepsilon$ greedy
在on-policy算法中,policy一般是soft的,整个policy整体上向一个deterministic policy偏移。
在$\varepsilon$ soft算法中,只要满足$\pi(a|s)\gt 0,\forall s\in S, a\in A$即可。
在$\varepsilon$ greedy算法中,用$\frac{\varepsilon}{|A(s)|}$的概率选择non-greedy的action,使用$1 -\varepsilon + \frac{\varepsilon}{|A(s)|}$的概率选择greedy的action。
$\varepsilon$ greedy是$\varepsilon$ soft算法中的一类,可以看成一种特殊的$\varepsilon$ soft算法。
本节介绍的on policy方法使用$\varepsilon$ greedy算法。
On-policy first visit MC
本节介绍的on policy MC算法整体的思路还是GPI,首先使用first visit MC估计当前policy的action value function。去掉exploring starting条件之后,为了保证exploration,不能直接对所有的action value进行贪心,使用$\varepsilon$ greedy算法保持exploration。
算法3 On policy first visit MC Control
$\varepsilon \gt 0$
初始化
$\qquad$用任意$\varepsilon$ soft算法初始化$\pi$
$\qquad$任意初始化$Q(s, a)\in R, \forall s\in S, \forall a \in A(s)$
$\qquad$Returns(s,a) $\leftarrow$ empty list, $\forall s\in S, \forall a \in A(s)$
Loop forever(for each episode)
$\qquad$根据policy $\pi$生成一个episode,$S_0,A_0,R_1,\cdots,S_{T-1},A_{T-1},R_T$
$\qquad G\leftarrow 0$
$\qquad$Loop for each step of episode,$t=T-1,T-2,\cdots,0$
$\qquad\qquad G\leftarrow \gamma G+R_{t+1}$
$\qquad\qquad$如果$S_t,A_t$没有在$S_0,A_0,\cdots, S_{t-1},A_{t-1}$中出现过
$\qquad\qquad\qquad$Returns($S_t,A_t$).append(G)
$\qquad\qquad\qquad Q(S_t,A_t) \leftarrow average(Returns(S_t, A_t)$
$\qquad\qquad\qquad A^{*}\leftarrow argmax_a Q(S_t,a)$
$\qquad\qquad\qquad$For all $a \in A(S_t) : $
$\qquad\qquad\qquad\qquad\pi(a|S_t)\leftarrow \begin{cases}1-\varepsilon+\frac{\varepsilon}{|A(S_t)|}\qquad if\ a = A^{*}\\ \frac{\varepsilon}{|A(S_t)|}\qquad a\neq A^{*}\end{cases}$
对于任意的$\varepsilon$ soft policy $\pi$,相对于$q_{\pi}$的$\varepsilon$ greedy算法至少和$\pi$一样好。用$\pi’$表示$\varepsilon$ greedy policy,对于$\forall s\in S$,都满足policy improvement theorem的条件:
\begin{align*}
q_{\pi}(s,\pi’(s))&=\sum_a\pi’(a|s)q_{\pi}(s,a)\\
&=\frac{\varepsilon}{|A(s)|} \sum_aq_{\pi}(s,a) + (1- \varepsilon) max_a q_{\pi}(s,a) \tag{2}\\
&\ge \frac{\varepsilon}{|A(s)|} \sum_aq_{\pi}(s,a) + (1-\varepsilon) \sum_a\frac{\pi(a|s) - \frac{\varepsilon}{|A(s)|}}{1-\varepsilon}q_{\pi}(s,a) \tag{3}\\
&=\frac{\varepsilon}{|A(s)|} \sum_aq_{\pi}(s,a) - \frac{\varepsilon}{|A(s)|} \sum_aq_{\pi}(s,a) + \sum_a \pi(a|s)\sum_aq_{\pi}(s,a)\\
&=v(s)
\end{align*}
式子2到式子3是怎么变换的,我有点没看明白!!!(不懂)。后来终于想明白了,式子3的第二项分子服从的是$\pi(a|s)$,而式子2的第二项这个$a$是新的$\pi’(a|s)$。
接下来证明,当$\pi$和$\pi’$都是optimal $\varepsilon$ policy的时候,可以取到等号。这个我看这没什么意思,就不证明了。。在p102。
Off-policy Prediction via Importance Sampling
所有的control方法都要面临一个问题:一方面需要选择optimal的action估计action value,另一方面需要exploration,不能一直选择optimal action,那么该如何控制这两个问题之间的比重。on-policy方法采样的方法是学习一个接近但不是optimal的policy保持exploriation。off-policy的方法使用两个policy,一个用于采样的behavior policy,一个用于evaluation的target policy。用于学习target policy的data不是target policy自己产生的,所以叫做off-policy learning。
on-policy vs off-policy
on policy更简单,off policy使用两个不同的policy,所以variance更大,收敛的更慢,但是off-policy效果更好,更通用。On-policy可以看成off-policy的特例,target policy和behaviour policy是相同的。Off-policy可以使用非学习出来的data,比如人工生成的data。
off-policy prediction problem
对于prediction problem,target policy和behaviour policy都是固定的。$\pi$是target policy,$b$是behaviour policy,我们要使用$b$生成的episode去估计$q_{\pi}$或者$v_{\pi}$。为了使用$b$生成的episodes估计$\pi$,需要满足一个假设,policy $\pi$中采取的action在$b$中也要能有概率被采取,即$\pi(a|s)\gt 0$表明$b(a|s) \gt 0$,这是coverage假设。
在control问题中,target policy通常是相对于当前action value的deterministic greedy policy,最后target policy是一个deterministic optimal policy而behaviour policy通常是$\varepsilon$ greedy的探索策略。
importance sampling和importance sampling ratio
很多off policy方法使用importance sampling,利用一个distribution的samples估计另一个distribution的value function。Importance sampling通过计算trajectoried在target和behaviour policy中出现的概率比值对returns进行加权,这个相对概率称为importance sampling ratio。给定以$S_t$为初始状态的sate-action trajectory,它在任何一个policy $\pi$中发生的概率如下:
\begin{align*}
&Pr\{A_t, S_{t+1},A_{t+1},\cdots,S_T|A_{t:T-1}\sim \pi,S_t\}\\
=&\pi(A_t|S_t)p(S_{t+1}|S_t,A_t)\pi(A_{t+1}|S_{t+1})\cdots p(S_T|S_{T-1},A_{T-1})\\
=&\prod_{k=t}^{T-1}\pi(A_k|S_k)p(S_{k+1}|S_k,A_k)
\end{align*}
其中$p$是状态转换概率,imporrance sampling计算如下:
$$\rho_{t:T-1}=\frac{\prod_{k=t}^{T-1} \pi(A_k|S_k)p(S_{k+1}|S_k,A_k)}{\prod_{k=t}^{T-1} b(A_k|S_k)p(S_{k+1}|S_k,A_k)}=\prod_{k=t}^{T-1}\frac{\pi(A_k|S_k)}{b(A_k|S_k}\tag{2}$$
因为p跟policy无关,所以可以直接消去。importance sampling ratio只和policies以及sequences有关。
根据behaviour policy的returns $G_t$,我们可以得到一个Expectation,即$\mathbb{E}[G_t|S_t=s]=v_b(s)$,显然,这是b的value function而不是$\pi$的value function,这个时候就用到了importance sampling,ratio $\rho_{t:T-1}$对b的returns进行转换,得到了另一个期望:
$$\mathbb{E}[\rho_{t:T-1}G_t|S_t=s]=v_{\pi}(s)\tag{3}$$
符号定义
假设我们想要从policy b 中的一些episodes中估计$v_{\pi}(s)$,
- 用$t$表示episode中的每一步,有些不同的是,$t$在不同episode之间是连续的,比如第$1$个episode有$100$个timesteps,第$2$个episode的timsteps从$101$开始。
- 用$J(s)$表示state $s$在不同episodes中第一次出现的$t$。
- 用$T(t)$表示从$t$所在那个episode的terminal timestep。
- 用$\left\{G_t\right\}_{t\in J(s)}$表示所有state $s$的return list。
- 用$\left\{\rho_{t:T(t)-1}\right\}_{t\in J(s)}$表示相应的importance ratio。
importance sampling
有两种importance sampling方法估计$v_{\pi}(s)$,一种是oridinary importance sampling,一种是weighted importance sampling。
oridinary importance sampling
直接对多个结果进行平均
$$V(s) = \frac{\sum_{t\in J(s)}\rho_{t:T(t)-1} G_t}{|J(s)|}\tag{4}$$
weighted importance sampling
对多个结果进行加权平均
$$V(s) = \frac{\sum_{t\in J(s)}\rho_{t:T(t)-1} G_t}{\sum_{t\in J(s)}\rho_{t:T(t)-1}}\tag{5}$$
异同点
为了比较这两种importance sampling的异同,考虑state s只有一个returns的first vist MC方法,在加权平均中,ratio会约分约掉,这个returns的expectation是$v_b(s)$而不是$v_{\pi}(s)$,是一个有偏估计;而普通平均,returns的expectation还是$v_{\pi}(s)$,是一个无偏估计,但是可能会很极端,比如ratio是$10$,就说明$v_{\pi}(s)$是$v_b(s)$的$10$倍,可能与实际相差很大。
在fisrt visit算法中,就偏差和方差来说。普通平均的偏差是无偏的,而加权平均的偏差是有偏的(逐渐趋向$0$)。普通平均的方差是unbounded,因为ratio可以是unbounded,而加权平均对于每一个returns来说,权重最大是$1$。事实上,假定returns是bounded,即使ratios的方差是infinite,加权平均的方差也会趋于$0$。实践中,加权平均有更小的方差,通常更多的被采用。
在every visit算法中,普通平均和加权平均都是有偏的,随着样本的增加,偏差也趋向于$0$。在实践中,因为every visit不需要记录哪个状态是否被记录过,所以要比first visit常用。
无穷大方差
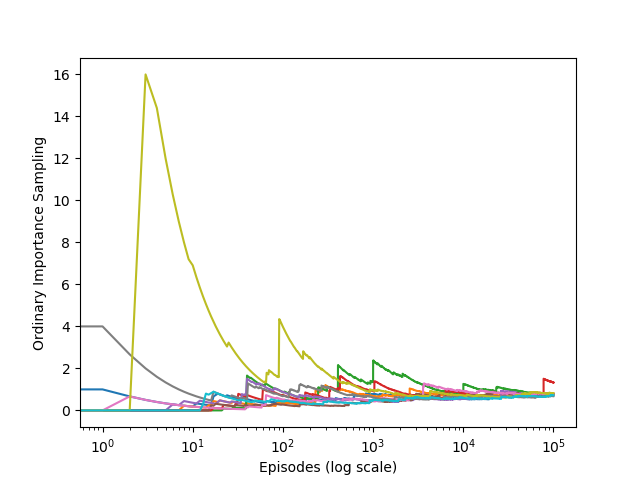
考虑一个例子。只有一个non-terminal state s,两个ation,left和right,right action是deterministic transition到termination,left action有$0.9$的概率回到s,有$0.1$的概率到termination。left action回到termination会产生$+1$的reward,其他操作的reward是$0$。所有target policy策略下的episodes都会经过一些次回到state s然后到达terminal state,总的returns是$1(\gamma = 1)$。使用behaviour policy等概率选择left和right action。
这个例子中returns的真实期望是$1$。first visit中weighted importance sampling中return的期望是$1$,因为behaviour policy中选择right的action 在target policy中概率为$0$,不满足之前假设的条件,所以没有影响。而oridinary importance sampling的returns期望也是$1$,但是可能经过了几百万个episodes之后,也不一定收敛到$1$。
接下来我们证明oridinary importance sampling中returns的variance是infinite。
$$Var(X) = \mathbb{E}\left[(X-\bar{X})^2\right] = \mathbb{E}\left[X^2-2\bar{X}X +\bar{x}^2\right]= \mathbb{E}\left[X^2\right]-\bar{X}^2 \tag{6}$$
如果mean是finite,只有当random variable的平方的Expectation为infinte时variance是infinte。所以,我们需要证明:
$$\mathbb{E}_b\left[\left(\prod_{t=0}^{T-1}\frac{\pi(A_t|S_t)}{b(A_t|S_t)}G_0\right)^2\right] \tag{7}$$
是infinte的。
这里我们按照一个episode一个episode的进行计算。但是需要注意的是,behaviour policy可以选择right action,而target policy只有left action,当behaviour policy选择right的话,ratio是$0$。我们只需要考虑那些一直选择left action回到state s,然后通过left action到达terminal state的episodes。按照下式计算期望,注意这个和上面用oridinary important ratio估计$v_{\pi}(s)$可不一样,上面是用采样估计$v_{\pi}(s)$,这个是计算真实的$v_{\pi}(s)$的期望,不对,是它的平方的期望。
\begin{align*}
\mathbb{E}_b\left[\left( \prod_{t=0}^{T-1}\frac{\pi(A_t|S_t)}{b(A_t|S_t)}G_0\right)^2\right] = & \frac{1}{2}\cdot 0.1 \left(\frac{1}{0.5}\right)^2\tag{长度为1的episode}\\
&+\frac{1}{2}\cdot 0.9\cdot\frac{1}{2}\cdot 0.1 \left(\frac{1}{0.5}\frac{1}{0.5}\right)^2\tag{长度为2的episode}\\
&+\frac{1}{2}\cdot 0.9\cdot \frac{1}{2} \cdot 0.9 \frac{1}{2}\cdot 0.1 \left(\frac{1}{0.5}\frac{1}{0.5}\frac{1}{0.5}\right)^2\tag{长度为3的episode}\\
&+ \cdots\\
=&0.1 \sum_{k=0}^{\infty}0.9^k\cdot 2^k \cdot 2\\
=&0.2 \sum_{k=0}^{\infty}1.8^k\\
=&\infty \tag{8}\
\end{align*}
Incremental Implementation
Monte Carlo prediction可以增量式实现,用episode-by-episode bias。
在on-policy算法中,$V_t$的估计通过直接对多个episode的$G_t$进行平均得到。
$$V_n(s) = \frac{G_1 + G_2 + \cdots + G_{n-1}}{n - 1} \tag{9}$$
其中$V_n(s)$表示在第$n$个epsisode估计的state $s$的value function,$n-1$表示采样得到的总共$n-$个episode,$G_1$表示每个episode中第一次遇到$s$时的Return。
在第$n+1$个episodes估计$V(s)$时:
\begin{align*}
V_{n+1}(s) &= \frac{G_1 + G_2 + \cdots + G_n}{n}\\
nV_{n+1}(s)&= G_1 + G_2 + \cdots + G_{n - 1} + G_n\tag{上式两边同时乘上n}\\
(n-1)V_n(s)&= G_1 + G_2 + \cdots + G_{n - 1}\tag{用n-1代替n}\\
nV_{n+1}(s)&= G_1 + G_2 + \cdots + G_{n - 1} + G_n\tag{分解V_{n+1}(s)}\\
&= (G_1 + G_2 + \cdots + G_{n - 1}) + G_n\\
&= (n-1)V_n(s) + G_n\\
\frac{nV_{n+1}(s)}{n}&= \frac{(n-1)V_n(s) + G_n}{n}\tag{上式两边同时除以n}\\
V_{n+1}(s)&= \frac{(n-1)V_n(s) + G_n}{n}\\
& = V_n(s) +\frac{G_n-V_n(s)}{n} \tag{10}
\end{align*}
这个更新规则的一般形式如下:
$$NewEstimate \leftarrow OldEstimate + StepSize \left[Target - OldEstimate\right] \tag{11}$$
表达式$\left[Target - OldEstimate\right]$是一个estimate error,通过向"Target"走一步减小error。这个"Target"给定了更新的方向,当然也有可能是noisy,在式子$10$中,target是第$n$个episode中state s的return。式子$10$的更新规则中StepSize$\frac{1}{n}$是在变的,一般我们叫它步长或者学习率,用$\alpha$表示。
在off-policy算法中,odrinary importance sampling和weighted importance sampling要分开。因为odirinary importance sampling只是对ratio缩放后的不同returns做了平均,还可以使用上面的公式。而对于weighted imporatance sampling,假设一系列episodes的returns是$G_1,G_2,\cdots, G_{n-1}$,对应的权重为$W_i$(比如$W_i=\rho_{t_i:T(t_i)-1}$),有:
$$V_n = \frac{\sum_{k=1}^{n-1}W_kG_k}{\sum_{k=1}^{n-1}W_k} \tag{11}$$
用$C_n$表示前$n$个episode returns的权重和,即$C_n=\sum_{k=1}^nW_k$,$V_n$的更新规则如下:
\begin{align*}
V_{n+1}&=\frac{\sum_{k=1}^{n}W_kG_k}{\sum_{k=1}^{n}W_k}\\
&=\frac{\sum_{k=1}^{n-1}W_kG_k + W_nG_n}{\sum_{k=1}^{n}W_k}\\
&=\frac{1}{\sum_{k=1}^{n}W_k} \cdot \left(\sum_{k=1}^{n-1}W_kG_k + W_nG_n\right)\\
&=\frac{1}{\sum_{k=1}^{n}W_k} \cdot \left(\frac{\sum_{k=1}^{n-1}W_kG_k}{\sum_{k=1}^{n-1}W_k}(\sum_{k=1}^{n-1}W_k) + W_nG_n\right)\\
&=\frac{1}{\sum_{k=1}^{n}W_k} \cdot \left(V_n\cdot(\sum_{k=1}^{n-1}W_k) + W_nG_n\right)\\
&=\frac{1}{\sum_{k=1}^{n}W_k} \cdot \left(V_n\cdot(\sum_{k=1}^{n-1}W_k + W_n - W_n) + W_nG_n\right)\\
&=\frac{1}{\sum_{k=1}^{n}W_k} \cdot \left(V_n\cdot(\sum_{k=1}^{n}W_k - W_n) + W_nG_n\right)\\
&=\frac{1}{\sum_{k=1}^{n}W_k} \cdot \left(V_n\cdot(\sum_{k=1}^{n}W_k) + W_nG_n - W_nV_n\right)\\
&=\frac{V_n\cdot(\sum_{k=1}^{n}W_k)}{\sum_{k=1}^{n}W_k} + \frac{W_nG_n-W_nV_n}{\sum_{k=1}^{n}W_k}\\
&=V_n + \frac{W_n}{C_n}(G_n-V_n)\\
\end{align*}
其中$C_0=0, C_{n+1} = C_n + W_{n+1}$,事实上,在$W_k=1$的情况下,即$\pi=b$时,上面的公式就变成了on-policy的公式。接下来给出一个episode-by-episode的MC policy evaluation incremental algorithm,使用的是weighted importance sampling。
Off-policy MC Prediction 算法
算法 4 Off-policy MC prediction(policy evaluation)
输入: 一个任意的target policy $\pi$
初始化,$Q(s,a)\in \mathbb{R}, C(s,a) = 0, \forall s\in S, a\in A(s)$
Loop forever (for each episode)
$\qquad$$b\leftarrow$ 任意覆盖target policy $\pi$的behaviour policy
$\qquad$用behaviour policy $b$生成一个episode,$S_0,A_0,R_1,\cdots, S_{T-1},A_{T-1},R_T$
$\qquad$$G\leftarrow 0$
$\qquad$$W\leftarrow 1$
$\qquad$FOR $t \in T-1,T-2,\cdots, 0$并且$W\neq 0$
$\qquad\qquad$$G\leftarrow G+\gamma R_{t+1}$
$\qquad\qquad$$W\leftarrow = W\cdot \frac{\pi(A_t|S_t)}{b(A_t|S_t)}$!!!原书中这个是放在最后一行的,我怎么觉得应该放在这里。。
$\qquad\qquad$$C(S_t, A_t)\leftarrow C(S_t, A_t)+W$
$\qquad\qquad$$Q(S_t, A_t)\leftarrow Q(S_t, A_t)+ \frac{W}{C(S_t,A_t)}(G_t-Q(S_t,A_t))$
$\qquad$END FOR
思考:这里怎么把它转换为first-visit的算法
Off-policy MC Control
这一节给出一个off-policy的MC control算法,target policy是greedy算法,而behaviour policy是soft算法,在不同的episode中可以采用不同的behaviour policy。
算法 5 Off-policy MC control
初始化,$Q(s,a)\in \mathbb{R}, C(s,a) = 0, \forall s\in S, a\in A(s), \pi(s)\leftarrow arg max_aQ(s, a)$
Loop forever (for each episode)
$\qquad$$b\leftarrow$ 任意覆盖target policy $\pi$的behaviour policy
$\qquad$用behaviour policy $b$生成一个episode,$S_0,A_0,R_1,\cdots, S_{T-1},A_{T-1},R_T$
$\qquad$$G\leftarrow 0$
$\qquad$$W\leftarrow 1$
$\qquad$for $t \in T-1,T-2,\cdots, 0$并且$W\neq 0$
$\qquad\qquad$$G\leftarrow G+\gamma R_{t+1}$
$\qquad\qquad$$C(S_t, A_t)\leftarrow C(S_t, A_t)+W$
$\qquad\qquad$$Q(S_t, A_t)\leftarrow Q(S_t, A_t)+ \frac{W}{C(S_t,A_t)}(G_t-Q(S_t, A_t)$
$\qquad\qquad\pi(s)\leftarrow arg max_aQ(S_t,a)$
$\qquad\qquad$if $A_t\neq\pi(S_t)$ then
$\qquad\qquad\qquad$break for循环
$\qquad\qquad$end if
$\qquad\qquad$$W\leftarrow = W\cdot \frac{1}{b(A_t|S_t)}$这个为什么放最后一行,我能理解要进行一下if判断,但是放在这里importance ratio不就不对了吗。。
$\qquad$end for
Discounting-aware Importance Sampling
这一节介绍了discounting的importance sampling,假设有$100$个steps的一个episode,$\gamma=0$,其实它的returns在第一步以后就确定了,后面的$99$步已经没有影响了,因为$\gamma=0$,这里就介绍了discount importance sampling。
…
Per-decision Importance Sampling
根据每一个Reward确定进行importance sampling,而不是根据每一个returns。
…
Summary
MC相对于DP的好处
- model-free
- sample比较容易
- 很容易focus在一个我们需要的subset上
- 不进行bootstrap
在MC control算法中,估计的是action-value fucntion,因为action value function能够在不知道model dynamic的情况下改进policy。