神经网络-dropout

发表于 | 更新于 | 分类于 | 评论数：

dropou是干什么的

Dropout 是一种正则化技术，通过学习鲁棒的特征来防止过拟合。

为什么会有过拟合

如果输入和正确输出之间有很复杂的映射关系，而网络又有足够多的隐藏单元去正确的建模，那么通常会用很多组权重都能在训练集上得到好的结果。但是每一组权重在测试集上的结果都比训练集差，因为它们只在训练集上训练了，而没有在测试集上训练。

什么是dropout

在网络中每一个隐藏单元的输出单元都有$0.5$的概率被忽略，所以每一个隐藏单元需要学会独立于其他的隐藏单元决定输出结果。

This technique reduces complex co-adaptations of neurons, since a neuron cannot rely on the presence of particular other neurons. It is, therefore, forced to learn more robust features that are useful in conjunction with many different random subsets of the other neurons. [0]

On each presentation of each training case, each hidden unit is randomly omitted from the network with a probability of 0.5, so a hidden unit cannot rely on other hidden units being present.[1]

Dropout stops the mechanism of training neurons of any layers as a family, so reduces co-adaptability.[3]

另一种方式可以把dropout看成对神经网络做平均。一种非常有效的减少测试误差的方法就是对一系列神经网络预测的结果取平均。理想的方式是训练很多个网络，然后分别在每个网络上进行测试，但是这样子的计算代价是很高的。随机的dropout让在合理的时间内训练大量不同的网络变得可能。当我们丢弃一个神经元的时候，它对loss函数没有任何贡献，所以在反向传播的时候，梯度为$0$，权值不会被更新。这就相当于我们对网络进行了一个下采样，训练过程的每次迭代中，采样网络的一部分进行训练，这样我们就得到了一个共享参数的集成模型。对于每一次训练，网络结构都是相同的，但是每次选择的参数都有很大可能是不同的，而且权重是共享的。

The neurons which are “dropped out” in this way do not contribute to the forward pass and do not participate in backpropagation. So every time an input is presented, the neural network samples a different architecture, but all these architectures share weights.

在测试的时候，使用"mean networks"，就是保留网络中所有的权重，但是要把激活函数的输出（activations)乘上$0.5$，因为相对训练的时候，每个神经元都有$0.5$的概率被激活，这个时候如果不乘上的话，最后就相当于测试的时候激活的神经元是训练时候的两倍。在实践中证明，这和对一系列经过dropout的网络取平均值的结果是很像的。（为什么就是两倍？）

Dropout can also be thought of as an ensemble of models that share parameters. When we drop a neuron, it has no effect on the loss function and thus the gradient that flows through it during backpropagation is effectively zero and so its weights will not get updated. This means that we are basically subsampling a part of the neural network and we are training it on a single example. In every iteration of training, we will subsample a different part of the network and train that network on the datapoint at that point of time. Thus what we have essentially is an ensemble of models that share some parameters.[3]

一个具有$N$个隐藏节点的网络，和一个用于计算类别标签的softmax输出层，使用mean networks就相当于对$2^N$个网络输出的标签概率做几何平均（并不是数学上的几何平均）。（为什么是几何平均？这里其实不是几何平均，只是一个等权重加权。）

a) The authors of the referenced article don’t use the ‘geometric mean’ of the predictions, but “an equally weighted geometric mean” of them.
b) They propose geometric mean over arithmetic mean for giving more value to more frequent data, probably according to the understanding by them of the underlying relations.
If, for example, you take the arithmetic mean of ${10, 10, 100}$, you get $40$, but if you take their geometric mean you get $\sqrt[3]{10000} \approx 21.54$, meaning the ‘odd’ measurement ($100$) plays a smaller role to the mean.
c) Even the geometric mean might be misleading, if the data are not assigned their true ‘weight’, meaning their occurrence or probability of occurrence, while assuring that this assignment of weights is equally important for all data.
Hence “equally weighted geometric mean”.[2]

如果采取dropout之后的网络输出不一样，那么mean network的输出能够保证赋值一个更高的可能性到正确标签。mean network的方根误差要比dropout网络方根误差的平均值要好，也就是说先对网络做平均然后计算误差要比先计算误差然后再平均要好。

实际上，$0.5$这个值不是固定的，可以根据不同情况进行微调。

why dropout works

其实这个和上面介绍中差不多，给出一种直观的解释。给一个例子[4]，有一个三层的神经网络，在下图中，红圈中的节点对于正确的输出起到了决定性的作用，在BP的过程中，它的权值不断增加，但是它可能在训练集上效果很好，但是测试集上很差。
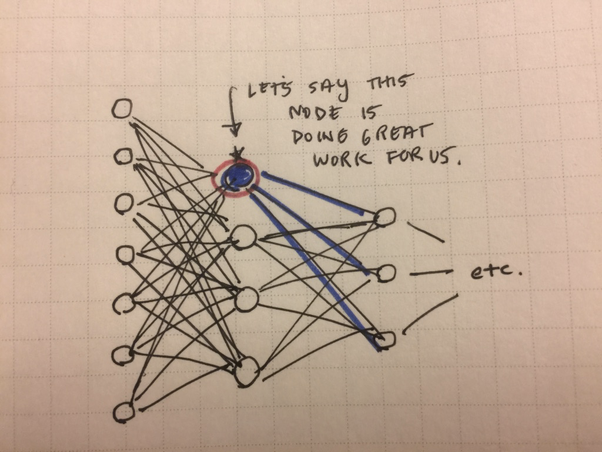
dropout
当采用了dropout以后，我们随意丢弃一些节点，如果把上图的关键节点丢了，那么网络必须重新学习其他的节点，才能够正确的进行分类。如下图，网络必须在另外可能没有丢弃的三个节点中选择一个用于正确分类。所以，这样子上图中的关键节点的作用就会被减轻，在新数据集上的鲁棒性可能就会更好。
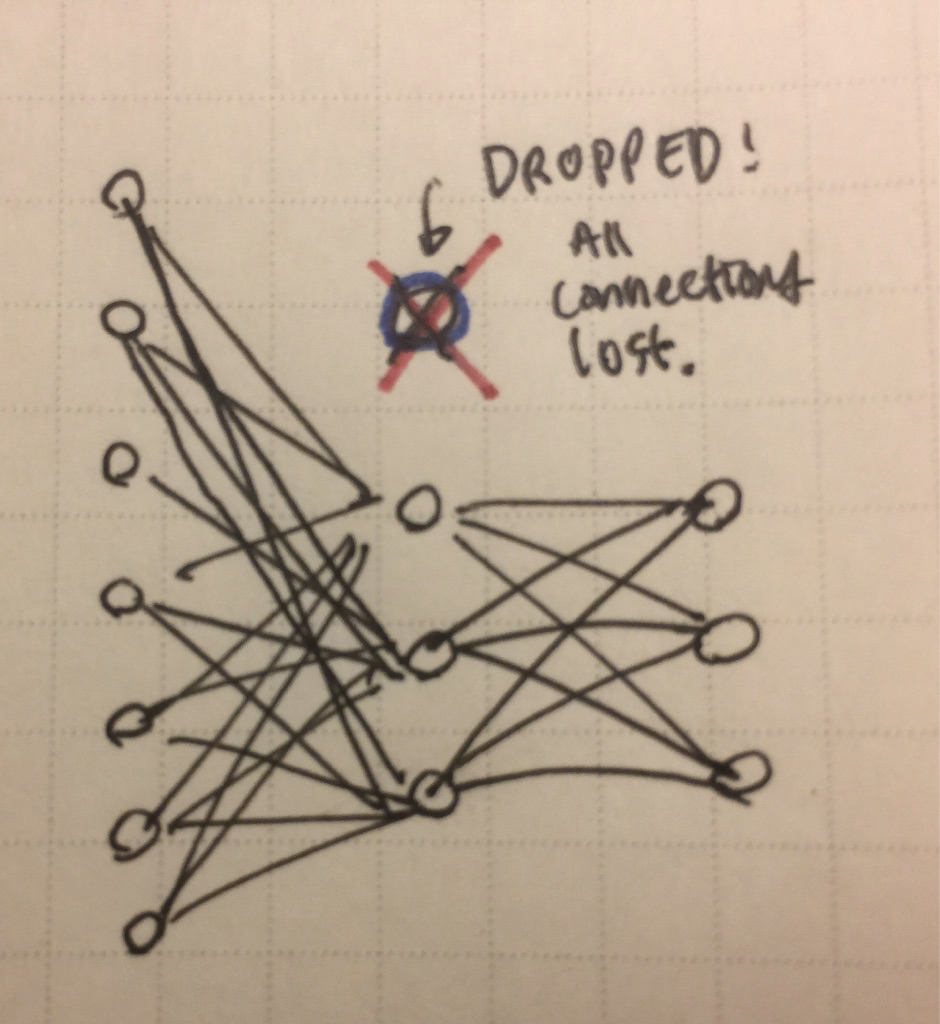
dropout

实现

numpy 实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
def forward(x, w1, w2, w3, training=False):
  z1 = np.dot(x, w1)
  y1 = np.tanh(z1)

  z2 = np.dot(y1, w2)
  y2 = np.dot(z2)
  # dropout in layer 2 
  if training:
     m2 = np.random.binomial(1, 0.5, size=z2.shape)
  else:
     m2 = 0.5

  y2 *= m2
  z3 = np.dot(y2, w3)
  y3 = z3
  return y1, y2, y3, m2

pytorch库

参考文献

1.https://arxiv.org/pdf/1207.0580.pdf
2.https://www.cs.toronto.edu/~hinton/absps/JMLRdropout.pdf
3.https://www.quora.com/What-is-dropout-in-deep-learning
4.https://www.quora.com/What-is-the-use-of-geometric-mean-in-dropout-neural-networks-It-says-that-by-approximating-an-equally-weighted-geometric-mean-of-the-predictions-of-an-exponential-number-of-learned-models-that-share-parameters
5.https://www.quora.com/Why-exactly-does-dropout-in-deep-learning-work
6.https://www.quora.com/How-does-the-dropout-method-work-in-deep-learning-And-why-is-it-claimed-to-be-an-effective-trick-to-improve-your-network
7.https://pgaleone.eu/deep-learning/regularization/2017/01/10/anaysis-of-dropout/