神经网络-激活函数

激活函数的一些问题

为什么要使用non-linear激活函数不使用linear激活函数？

fnn
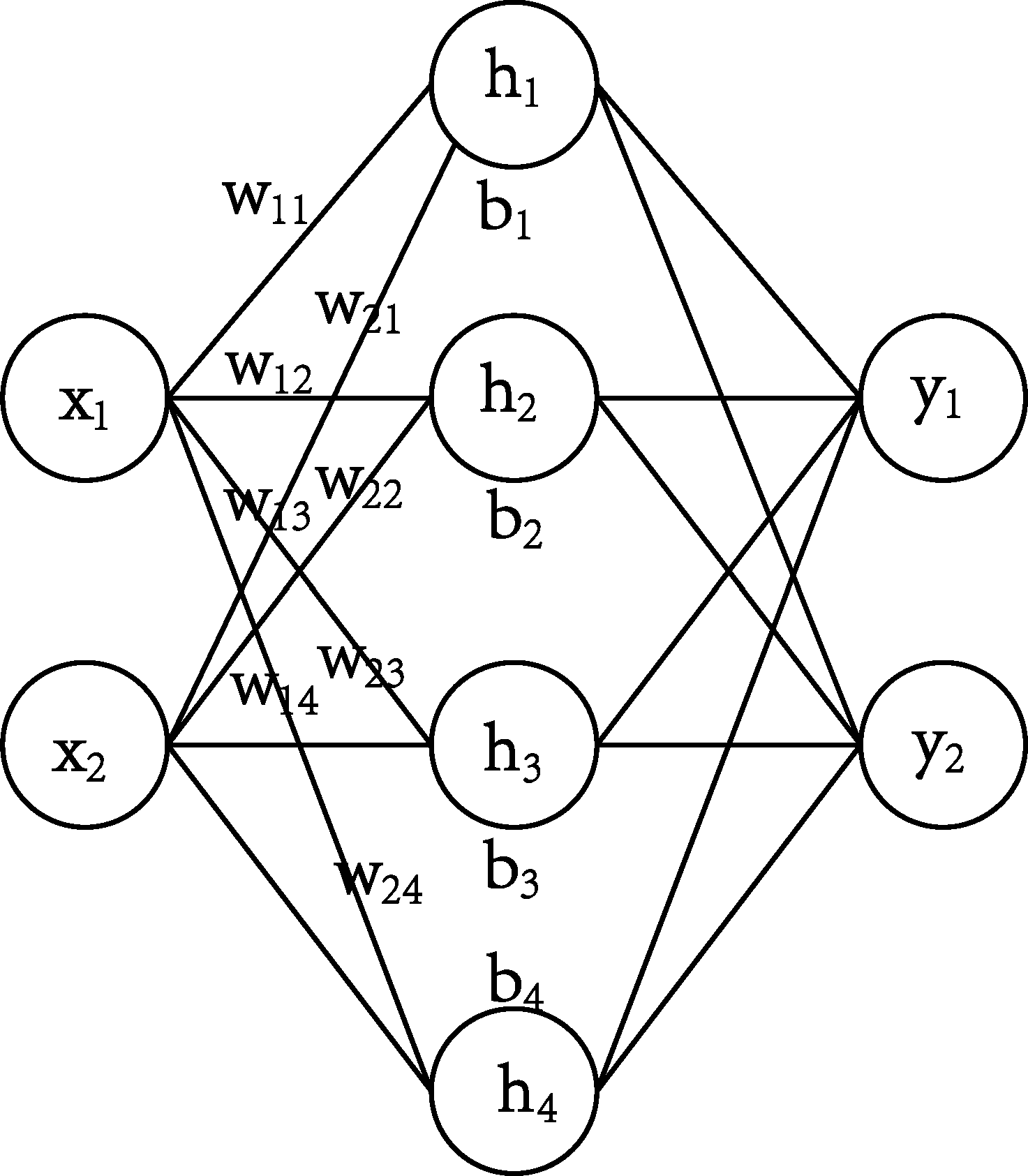
给定一个如图所示的前馈神经网络。有一个输入层，一个隐藏层，一个输出层。输入是$2$维的，有$4$个隐藏单元，输出是$2$维的。
则：$ \hat{f}(x) = \sigma(w_1x+b_1)w_2 + b_2$
这里$\sigma$是一个线性的激活函数，不妨设$\sigma(x) = x$。
那么就有：
\begin{align*}
\hat{f}(x) &= \sigma(w_1x+b_1)w_2 + b_2\
&= (w_1x+b_1)w_2 + b_2\
&= w_1w_2x + w_2b1 + b_2\
&= (w_1w_2) x + (w_2b1 + b_2)\
&= w’ x + b’
\end{align*}
因此，当使用线性激活函数的时候，我们可以把一个多层感知机模型化简成一个线性模型。当使用线性激活函数时，增加网络的深度没有用，使用线性激活函数的十层感知机和一层感知机没有区别，并不能增加网络的表达能力。因为任意两个仿射函数的组合还是仿射函数。

为什么ReLU激活函数是non-linear的？

ReLU的数学表达形式如下：
$$g(x) = max(0, x)$$
首先考虑一下什么是linear function,什么是non-linear function。在微积分上，平面内的任意一条直线是线性函数，否则就是非线性函数。
考虑这样一个例子，输入数据的维度为$1$，输出数据的维度也为$1$，用$g(ax+b)$表示ReLU激活函数。如果我们使用两个隐藏单元，那么$h_1(x) = g(x)+g(-x)$可以用来表示$f(x)=|x|$，而函数$|x|$是一个非线性函数，函数图像如下所示。

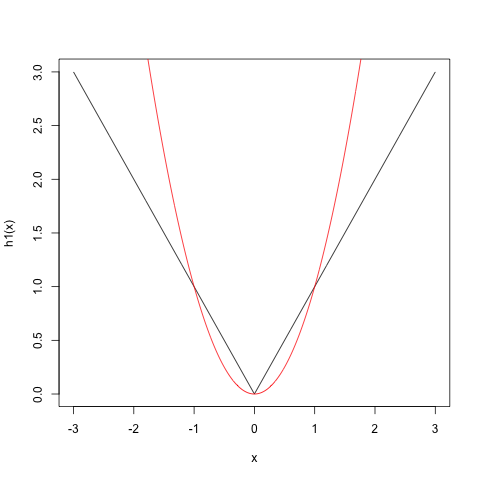
我们还可以用ReLU逼近二次函数$f(x) = x^2$，如使用函数$h_2(x) = g(x) + g(-x) + g(2x-2) + g(2x+2)$逼近二次函数，对应的图像如下。
h_2(x)
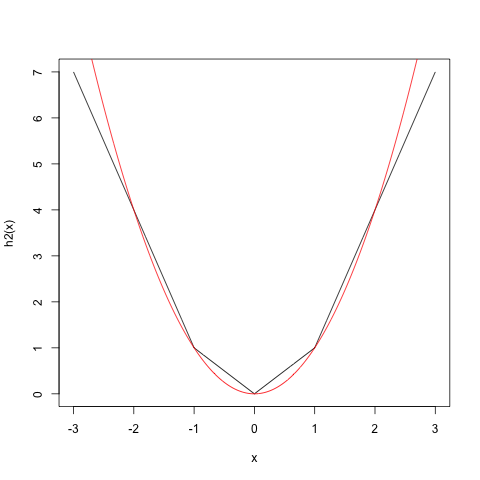
使用的项越多，最后近似出来的图像也就和我们要逼近的二次函数越像。
同理，可以使用ReLU激活函数去逼近任意非线性函数。

为什么ReLU比sigmod还有tanh激活函数要好？

ReLU收敛的更快，因为梯度更大。
当CNN的层数越来越深的时候，实验表明，使用ReLU的CNN要比使用sigmod或者tanh的CNN训练的更容易，更快收敛。
为什么会这样，目前有两种理论，见参考文献[4]。
第一个，$tanh(x)$有梯度消散问题(vanishing gradient)。当$x$趋向于$\pm\infty$时，$tanh(x)$的导数趋向于$0$。如下图所示。

Vanishing gradients occur when lower layers of a DNN have gradients of nearly 0 because higher layer units are nearly saturated at -1 or 1, the asymptotes of the tanh function. Such vanishing gradients cause slow optimization convergence, and in some cases the final trained network converges to a poor local minimum.

One way ReLUs improve neural networks is by speeding up training. The gradient computation is very simple (either 0 or 1 depending on the sign of x). Also, the computational step of a ReLU is easy: any negative elements are set to 0.0 – no exponentials, no multiplication or division operations.

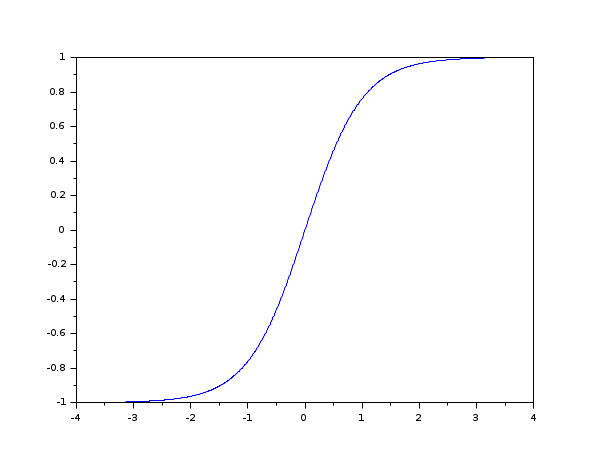
tanh(x)
ReLU是non-saturating nonlinearity的激活函数，sigmod和tanh是saturating nonlinearity激活函数，会将输出挤压到一个区间内。

f是non-saturating 当且仅当$|lim_{z\rightarrow -\infty} f(z)| \rightarrow + \infty$或者$|lim_{z\rightarrow +\infty} f(z)| \rightarrow + \infty$

tanh和sigmod将输入都挤压在某一个很小的区间内，比如(0,1)，输入发生很大的变化，经过激活函数以后变化很小，经过好几层之后，基本上就没有差别了。而当网络很深的时候，反向传播主要集中在后几层，而输入层附近的权值没办法好好学习。而对于ReLU来说，任意深度的神经网络，都不存在梯度消失。

第二种理论是说有一些定理能够证明，在某些假设条件下，局部最小就是全局最小。如果使用sigmod或者tanh激活函数的时候，这些假设不能成立，而使用ReLU的话，这些条件就会成立。

为什么发生了梯度消失以后训练结构很差？

我的想法是，

参考文献