convex optimization chapter 2 Convex sets

仿射集(affine sets)和凸集(convex sets)

直线(line)和线段(line segmens)

假设$x_1,x_2 \in \mathbb{R}^n $是n维空间中不重合$(x_1 \ne x_2)$的两点，给定：
$$y = \theta x_1 + (1 - \theta)x_2,$$
当$\theta\in R$时，$y$是经过点$x_1$和点$x_2$的直线。当$\theta=1$时，$y=x_1$,当$\theta=0$时，$y=x_2$。当$\theta\in[0,1]$时，$y$是$x_1$和$x_2$之间的线段(line segment)。把$y$改写成如下形式： $$y = x_2 + \theta(x_1 - x_2)$$，可以给出另一种解释，$y$是点$x_2$和方向$x_1 - x_2$(从$x_2$到$x_1$的方向)乘上一个缩放因子$\theta$的和。
如下图所示，可以将y看成$\theta$的函数。
line_line-segment

仿射集(affine sets)

仿射集的定义

给定一个集合$C\subset \mathbb{R}^n $,如果经过$C$中任意两个不同点的直线仍然在$C$中，那么$C$就是一个仿射集。即，对于任意$x_1,x_2\in C$和$\theta\in R$，都有$\theta x_1 + (1 - \theta)x_2 \in C$。换句话说，给定线性组合的系数和为$1$，$C$中任意两点的线性组合仍然在$C$中，我们就称这样的集合是仿射的(affine)。

仿射组合(affine combination)

我们可以把两个点的线性组合推广到多个点的线性组合，这里称它为仿射组合。
仿射组合的定义：给定$\theta_1+\cdots+\theta_k = 1$,则$\theta_1 x_1 + \cdots + \theta_k x_k$是点$x_1,\cdots,x_k$的仿射组合(affine combination)。
根据仿射集的定义，一个仿射集(affine set)包含集合中任意两个点的仿射（线性）组合，那么可以推导出仿射集包含集合中任意点（大于等于两个）的仿射组合，即：如果$C$是一个仿射集，$x_1,\cdots,x_k\in C$,且$\theta_1 x_1 + \cdots + \theta_k x_k = 1$,那么点$\theta_1 x_1 + \cdots + \theta_k x_k$仍然属于$C$。

仿射集的子空间(subspce)

如果$C$是一个仿射集，$x_0 \in C$,那么集合
$$V = C - x_0 = {x - x_0\big|x \in C}$$
是一个子空间(subspace),因为$V$是加法封闭和数乘封闭的。
证明：
假设$v_1, v_2 \in V$，并且$\alpha,\beta \in R$。
要证明V是一个子空间，那么只需要证明$\alpha v_1 + \beta v_2 \in V$即可。
因为$v_1, v_2 \in V$，则$v_1+x_0, v_2+x_0 \in C$。
而$x_0 \in C$，所以有
$$\alpha(v_1+x_0) + \beta(v_2+x_0) + (1 - \alpha - \beta)x_0 \in C$$
即：
\begin{align*}
\alpha v_1 + \beta v_2 + (\alpha + \beta + 1 - \alpha - \beta)x_0 &\in C\\
\alpha v_1 + \beta v_2 + x_0 &\in C
\end{align*}
所以$\alpha v_1 + \beta v_2 \in V$。
所以，仿射集$C$可以写成：
$$C = V + x_0 = { v + x_0\big| v \in V},$$
即，一个子空间加上一个偏移(offset)。而与仿射集$C$相关的子空间$V$与$x_0$的选择无关，即$x_0$可以为$C$中任意一点。

示例

线性方程组的解。一个线性方程组的解可以表示为一个仿射集:$C={x\big|Ax = b}$,其中 $A\in \mathbb{R}^{m \times n}, b \in \mathbb{R}^m $。
证明：
设$x_1, x_2 \in C$,即$Ax_1 = b, Ax_2 = b$。对于任意$\theta \in R$,有:
\begin{align*}
A(\theta x_1 + (1-\theta x_2) &= \theta Ax_1 + (1-\theta)Ax_2\\
&= \theta b + (1 - \theta) b\\
&= b \end{align*}
所以线性方程组的解是一个仿射组合：$\theta x_1 + (1 - \theta) x_2$，这个仿射组合在集合$C$中，所以线性方程组的解集$C$是一个仿射集。
和该仿射集$C$相关的子空间$V$是$A$的零空间(nullspace)。因为仿射集$C$中的任意点都是方程$Ax = b$的解，而$V = C - x_0 = {x - x_0\big|x \in C}$，有$Ax = b, Ax_0 = b$，则$Ax - Ax_0 = A(x - x_0) = b - b = 0$，所以$V$是$A$的零空间。

仿射包(affine hull)

给定集合$C\subset \mathbb{R}^n $，集合中点的仿射组合称为集合$C$的仿射包(affine hull),表示为$aff C$:
$aff C = {\theta_1 x_1 + \cdots + \theta_k x_k\big| x_1,\cdots,x_k \in C, \theta_1 + \cdots + \theta_k = 1}$
集合$C$可以是任意集合。仿射包是包含集合$C$的最小仿射集（一个集合的仿射包只有一个，是不变的）。即如果$S$是任意仿射集，满足$C\subset S$，那么有$aff C \subset S$。或者说仿射包是所有包含集合$C$的仿射集的交集。

仿射纬度(affine dimension)和相对内部(relative interior)

拓扑(topology)

拓扑(topology)，开集(open sets),闭集(close sets),内部(interior),边界(boundary),闭包(closure),邻域(neighbood),相对内部(relative interior)
同一个集合可以有很多个不同的拓扑。

定义

给定一个集合$X$,$\tau$是$X$的一系列子集，如果$\tau$满足以下条件：

空集(empty set)和全集X都是$\tau$的元素;
$\tau$中任意元素的并集(union)仍然是$\tau$的元素;
$\tau$中任意有限多个元素的交集(intersection)仍然是$\tau$中的元素。

则称$\tau$是集合$X$上的一个拓扑。
如果$\tau$是$X$上的一个拓扑，那么$(X,\tau)$对称为一个拓扑空间(topological space)。
如果$X$的一个子集在$\tau$中，这个子集被称为开集(open set)。
如果$X$的一个子集的补集是在$\tau$中，那么这个子集是闭集(closed set)。
$X$的子集可能是开集，闭集，或者都是，都不是。
空集和全集是开集，也是闭集（定义）。

示例

给定集合$X={1,2,3,4}$, 集合$\tau = { {},{1,2,3,4} }$就是$X$上的一个拓扑。
给定集合$X={1,2,3,4}$, 集合$\tau = { {},{1}, {3,4},{1,3,4},{1,2,3,4} }$就是$X$上的另一个拓扑。
给定集合$X={1,2,3,4}$, $X$的幂集(power set)也是$X$上的另一个拓扑。

通常如果不说的话，默认是在欧式空间(1维，2维,…,n维欧式空间)的拓扑，即欧式拓扑。以下讲的一些概念是在欧式空间的拓扑（通常拓扑）上的定义和一般拓扑直观上可能不太一样，但实际上意义是相同的。

$\epsilon-disc$或$\epsilon$邻域

定义

给定$x\in \mathbb{R}^n $以及$\epsilon\gt 0$，集合
$$D(x,\epsilon) = {y\in \mathbb{R}^n \big|d(x,y) \lt \epsilon}$$
称为关于$x$的$\epsilon-disc$或者$\epsilon$邻域(neighbood)或者$\epsilon$球(ball)。即所有离点$x$距离小于$\epsilon$的点$y$的集合。

开集(open sets)

定义

给定集合$A\subset \mathbb{R}^n $，对于$A$中的所有元素，即$\forall x\in A$，都存在$\epsilon \gt 0$使得$D(x,\epsilon)\subset A$，那么就称该集合是开的。
即集合$A$中所有元素的$spsilon$邻域都还在集合$A$中（定理$1$）。
注意：必须满足$\epsilon \gt 0$

定理

定理$1$ $epsilon$邻域是开集

在$\mathbb{R}^n $中，对于一个$\epsilon \gt 0, x\in \mathbb{R}^n $,那么集合$x$的$\epsilon$邻域$D(x,\epsilon)$是开的，给定一个$\epsilon$，能找到一个更小的$epsilon$邻域。

定理$2$

$\mathbb{R}^n $中有限个开子集的交集是$\mathbb{R}^n $的开子集。
$\mathbb{R}^n $中任意个开子集的并集是$\mathbb{R}^n $的开子集。

注意：任意开集的交可能不是开集，一个点不是开集，但是它是所有包含它的开集的交。

示例

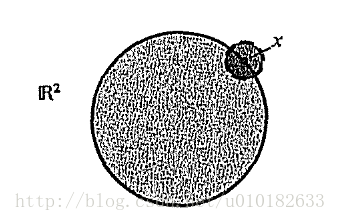
unit_circle

$\mathbb{R}^2 $中的不包含边界的球是开的，如图。
考虑一个$\mathbb{R}^1 $中的开区间，如$(0,1)$，它是一个开集，但是如果把它放在二维欧式空间中(是x轴上的一个线段)，它不是开的，不满足定义，所以开集是必须针对于某一个给定的集合$X$。
$\mathbb{R}^2 $上的包含边界的单位圆$X = {x\in \mathbb{R}^2 \big||x|\le 1}$不是开的。因为边界上的点$x$不满足$\epsilon \gt 0, D(x,\epsilon) \subset X$。
集合$S={(x,y) \in \mathbb{R}^2 \big|0 \lt x \lt 1}$是开集。对于每个点$(x,y)\in S$,我们可以画出半径$r = min{x,1-x}$的邻域并且其全部含于$S$，所以$S$是开集。
集合$S={(x,y) \in \mathbb{R}^2 \big|0 \lt x \le 1}$不是开集。因为点$(1,0) \in S$的邻域包含点$(x,0)$,其中$x\gt 1$。

内部(interior)

定义

给定集合$A\subset \mathbb{R}^n $,点$x \in A$，如果有一个开集$U$使得$x \in U\subset A$,那么该点就称为$A$的一个内点。或者说对于$x\in A$，有一个$\epsilon \gt 0$使得$D(x,\epsilon)\subset A$。$A$的所有内点组成的集合叫做$A$的内部(interior)，记做$int(A)$。

属性

集合内部可能是空的，单点的内部就是空的。
单位圆的内部是不包含边界的单位圆。
事实上$A$的内部是$A$所有开子集的并，由开集的定理得$A$的内部是开的，且$A$的内部是$A$的最大的开集。
当且仅当$A$的内部等于$A$的时候，$A$是开集（$A$可能是闭集）。
只需要寻找集合内$\epsilon$邻域还在这个集合内的点即可。

示例

给定集合$S={(x,y)\in \mathbb{R}^2 \big| 0 \lt x \le 1}$，$int(S) = {(x,y)\big|0 \lt x \lt 1}$。因为区间$(0,1)$中的点都满足它们的$\epsilon$邻域在$S$中。
$int(A) \cup int(B) \ne int(A\cup B)$。在实数轴上，$A=[0,1],B=[1,2]$，那么$int(A) = (0,1),int(B) = (1,2)$，所以$int(A) \cup int(B) = (0,1)\cup (1,2) = (0,2)\backslash {1}$，而$int(A\cup B) = int[0,2] = (0,2)$。

闭集(closed set)

定义

对于$\mathbb{R}^n $中的集合$B$，如果它在$\mathbb{R}^n $的补（即集合$\mathbb{R}^n \backslash B$）是开集，那么它是闭集。
单点是闭集。含有边界的单位圆组成的集合是闭集，因为它的补集不包含边界。一个集合可能既不是开集也不是闭集。例如，在一维欧几里得空间，半开半闭区间（如$(0,1]$）既不是开集也不是闭集。

定理

$\mathbb{R}^n $中有限个闭子集的并是闭集。
$\mathbb{R}^n $中任意个闭子集的交是闭集。

这个定理是从开集的定理中得出的，在对开集取补变成闭集时候，并与交相互变换即可。

示例

给定集合$S={(x,y) \in \mathbb{R}^2 \big| 0 \lt x \le 1, 0 \lt y \lt 1}$，$S$不是闭集。因为目标区域的下边界不在S中。
给定集合$S={(x,y) \in \mathbb{R}^2 \big| x^2 +y^2 \le 1}$，$S$是闭集，因为它的闭集是$\mathbb{R}^2 $中的开集。
$\mathbb{R}^n $中任何有限集是闭集。因为单点是闭集，有限集可以看成很多个单点的并，由定理$1$可以得出。

聚点(accumulation point)

定义

对于点$x\in \mathbb{R}^n $，如果包含$x$的每个开集$U$包含不同于$x$但依然属于集合$A$中的点，那么就称$x$是$A$的一个聚点(accumulation points)，也叫聚类点(cluster points)。**注意这里是包含集合$A$中的点，而不是全部是集合$A$中的点，所以集合的聚点不一定必须在集合中。**如，在一维欧式空间中，单点集合没有聚点，开区间$(0,1)$的聚点是$[0,1]$，${0,1}$不在区间内，但是是聚点。
此外，$x$是聚类点等价于：对于每个$\epsilon \gt 0$，$D(x,\epsilon)$包含$A$中的某点$y$且$y\ne x$。

定理

当且仅当集合$S$的所有聚点属于$S$时，$S\subset \mathbb{R}^n $是闭集。

示例

给定集合$S={x\in R\big|x\in [0,1]且x是有理数}$，$S$的聚点为$[0,1]$中所有点。任何不属于$[0,1]$的点都不是聚点，因为这类点有一个包含它的$\epsilon$邻域与$[0,1]$不相交。
给定集合$S={(x,y)\in \mathbb{R}^2 \big| 0 \le x\le 1\ or\ \ x = 2}$, 它的聚点是它本身，因为它是闭集。
给定集合$S={(x,y)\in \mathbb{R}^2 \big|y \lt x^2 + 1}$，S的聚点为集合${(x,y)\in \mathbb{R}^2 \big|y \le x^2 + 1}$，

闭包(closure)

定义

给定集合$A\subset \mathbb{R}^n $,集合$A$的闭包$cl(A)$定义成所有包含$A$的闭集的交，所以$cl(A)$是一个闭集。定价的定义是给定集合$A$，包含$A$的最小闭集叫做这个集合$X$的闭包(closure)，用$cl(A)$或者${\overline{A}}$表示。

定理

给定$A\subset \mathbb{R}^n $，那么$cl(A)$由$A$和$A$的所有聚点组成。

示例

$R$中$S=[0,1)\cup {2}$的闭包是$[0,1]$和${2}$。$S$的聚点是$[0,1]$，再并上$S$得到$S$的闭包是$[0,1]\cup{2}$。
对于任意$S\subset \mathbb{R}^n $，$\mathbb{R}^n \backslash cl(S)$是开集。因为$cl(S)$是闭集，所以它的补集是开集。
$cl(A\cap B) \ne cl(A)\cap cl(B)$。比如$A=(0,1),B(1,2),cl(A)=[0,1],cl(B)=[1,2]$,$A\cap B = \varnothing$,$cl(A\cap B) = \varnothing$,而$cl(A)\cap cl(B) = {1}$。

边界(boundary)

定义

对于$\mathbb{R}^n $中的集合$A$，边界定义为集合：
$bd(A) = cl(A)\cap cl(\mathbb{R}^n \backslash A)$
即集合$A$的补集的闭包和$A$的闭包的交集，所以$bd(A)$是闭集。$bd(A)$是$A$与$\mathbb{R}^n \backslash A$之间的边界。

定理

给定$A\subset \mathbb{R}^n $，当且仅当对于每个$\epsilon \gt 0$，$D(x,\epsilon)$包含$A$与$\mathbb{R}^n \backslash A$的点，$x\in bd(A)$。

示例

给定集合$S={x\in R\big|x\in [0,1],x是有理数}$，$bd(S) = [0,1]$。因为对于任意$\epsilon \gt 0, x\in [0,1],D(x,\epsilon) = (x-\epsilon, x+\epsilon)$包含有理数和无理数，即x是有理数和无理数之间的边界。
给定$x\in bd(S)$，$x$不一定是聚点。给定集合$S = {0} \subset R$，$bd(S) = {0}$，但是单点没有聚点。
给定集合$S={(x,y)\in \mathbb{R}^2 \big| x^2 -y^2 \gt 1 }$，$bd(S)={(x,y)\big|x^2 - y^2 = 1}$。

仿射维度(affine dimension)

定义

给定一个仿射集$C$，仿射维度是它的仿射包的维度。
仿射维度和其他维度的定义不总是相同的，具体可以看以下的示例。

示例

给定一个二维欧几里得空间的单位圆，${x\in C\big|x_1^2 +x_2^2 =1}$。它的仿射包是整个$\mathbb{R}^2$，所以二维平面的单位圆仿射维度是$2$。但是在很多定义中，二维平面的单位圆的维度是$1$。

相对内部(relative interior)

给定一个集合$C\subset \mathbb{R}^n $，它的仿射维度可能小于$n$，这个时候仿射集$aff\ C \ne \mathbb{R}^n $。

定义

给定集合$C$，相对内部的定义如下：
$relint\ C = {x\in C\big|(B(x,r)\cup aff\ C) \subset C, \exists \ r \gt 0}.$
就是集合$C$内所有$\epsilon$球在$C$的仿射集内的点的集合。
其中$B(x,r)={y \big|\Vert y- x\Vert \le r}$，是以$x$为中心，以$r$为半径的圆。这里的范数可以是任何范数，它们定义的相对内部是相同的。

示例

给定一个$\mathbb{R}^3 $空间中$(x_1,x_2)$平面上的正方形，$C={x\in \mathbb{R}^3 \big|-1 \le x_1 \le 1, -1\le x_2 \le 1, x_3 = 0}$。它的仿射包是$(x_1,x_2)$平面，$aff\ C = {x\in \mathbb{R}^3 \big|x_3=0}$。$C$的内部是空的，但是相对内部是：
$relint\ C = {x \in \mathbb{R}^3 \big|-1 \le x_1 \le 1, -1\le x_2 \le 1,x_3=0}$。

相对边界(relative boundary)

定义

给定集合$C$，相对边界(relative boundary)定义为$cl\ C \backslash relint\ C$，其中$cl\ C$是集合$C$的闭包(closure)。

示例

对于上例（相对内部的示例）来说，它的边界(boundary)是它本身。它的相对内部是边框，${x\in \mathbb{R}^3 \big|max{|x_1|,|x_2|}=1,x_3=0}$。

凸集(convex sets)

凸集定义

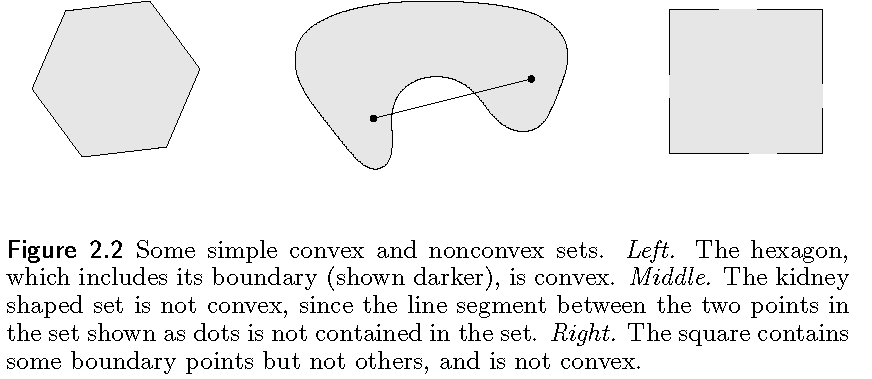
给定一个集合$C$，如果集合$C$中经过任意两点的线段仍然在$C$中，这个集合就是一个凸集。
给定$\forall x_1,x_2 \in C, 0 \le \theta \le 1$，那么我们有$\theta x_1 + (1-\theta)x_2 \in C$。
每一个仿射集都是凸的，因为它包含经过任意两个不同点的直线，所以肯定就包含过那两个点的线段。

凸组合(convex combination)

给定$k$个点$x_1,x_2,\cdots,x_k$，如果具有$\theta_1 x_1 + \cdots, \theta_k x_k$形式且满足$\theta_1 + \cdots + \theta_k=1, \theta_i \ge 0,i=1,\cdots,k$,那么就称这是$x_1,\cdots,x_k$的一个凸组合。
当且仅当一个集合包含其中所有点的凸组合，这个集合是一个凸集。点的一个凸组合可以看成点的混合或者加权，$\theta_i$是第$i$个点$x_i$的权重。
凸组合可以推广到无限维求和，积分，概率分布等等。假设$\theta_1,\theta_2,\cdots$满足：
$$\theta_i \le 0, i = 1,2,\cdots, \sum_{i=1}^{\infty}\theta_i = 1$$
并且$x_1,x_2,\cdots \in C$，$C\subset \mathbb{R}^n $是凸的，如果(series)$\sum_{i=1}^{\infty} \theta_i x_i$收敛，那么$\sum_{i=1}^{\infty} \theta_i x_i \in C$。
更一般的，假设概率分布$p$，$\mathbb{R}^n \rightarrow R$满足$p(x)\le 0 for\ all\ x\in C, \int_{C}p(x)dx = 1$,其中$C\subset \mathbb{R}^n $是凸的，如果$\int_{C}p(x)xdx$存在的话，那么$\int_{C}p(x)xdx\in C$。

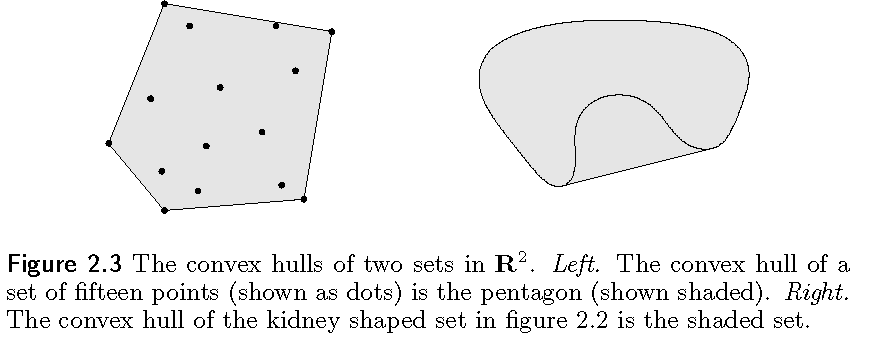
凸包(convex hull)

给定一个集合$C$，凸包的定义为包含集合$C$中所有点的凸组合的结合，记为$conv\ C$，公式如下：
$conv\ C = {\theta_1 x_1 + \cdots + \theta_k x_k\big|x_i \in C, \theta_i \ge 0, i = 1,\cdots,k,\theta_1 +\cdots + \theta_k = 1}$
任意集合都是有凸包的。一个集合的凸包总是凸的。集合$C$的凸包是包含集合$C$的最小凸集。如果集合$B$是任意包含$C$的凸集，那么$conv\ C \subset B$。

示例

figure 2.2
figure 2.3

锥(cones)

锥(cones)和凸锥(convex cones)的定义

给定集合$C$，如果$\forall x \in C, \theta \ge 0$，都有$\theta x\in C$，这样的集合就称为一个锥(cone)，或者非负同质(nonnegative homogeneour)。
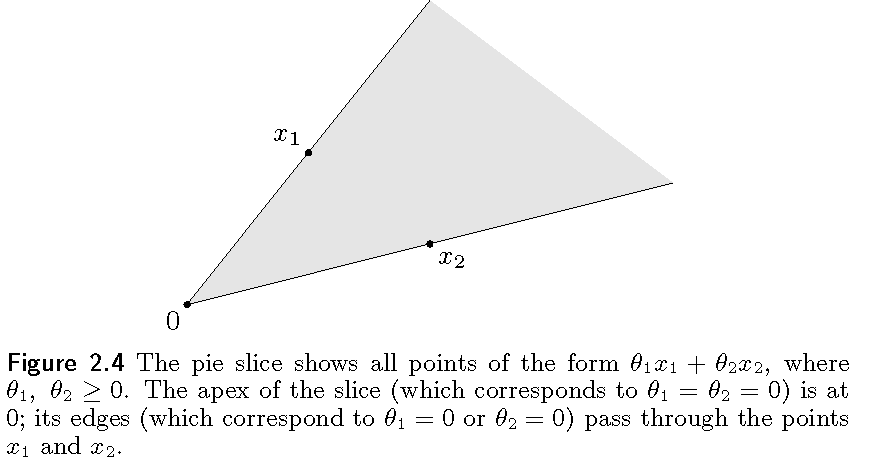
一个集合$C$如果既是锥又是凸的，那这个集合是一个凸锥(convex cone)，即：$\forall x_1,x_2 \in C, \theta_1,\theta_2 \ge 0$,那么有$\theta_1 x_1+\theta_2 x_2 \in C$。几何上可以看成经过顶点为原点，两条边分别经过点$x_1$和$x_2$的$2$维扇形。

锥组合(conic combination)

给定$k$个点$x_1,x_2,\cdots,x_k$，如果具有$\theta_1 x_1 + \cdots, \theta_k x_k$形式且满足$\theta_i \ge 0,i=1,\cdots,k$,那么就称这是$x_1,\cdots,x_k$的一个锥组合(conic combination)或者非负线性组合(nonnegative combination)。
给定集合$C$是凸锥，那么集合$C$中任意点$x_i$的锥组合仍然在集合$C$中。反过来，当且仅当集合$C$包含它的任意元素的凸组合时，这个集合是一个凸锥(convex cone)。

锥包(conic hull)

给定集合$C$，它的锥包(conic hull)是集合$C$中所有点的锥组合。即：
$conic\ C = {\theta_1 x_1 + \cdots + \theta_k x_k\big|x_i \in C, \theta_i \ge 0, i = 1,\cdots,k}$
集合$C$的锥包是包含集合$C$的最小凸锥。

示例

figure 2.4
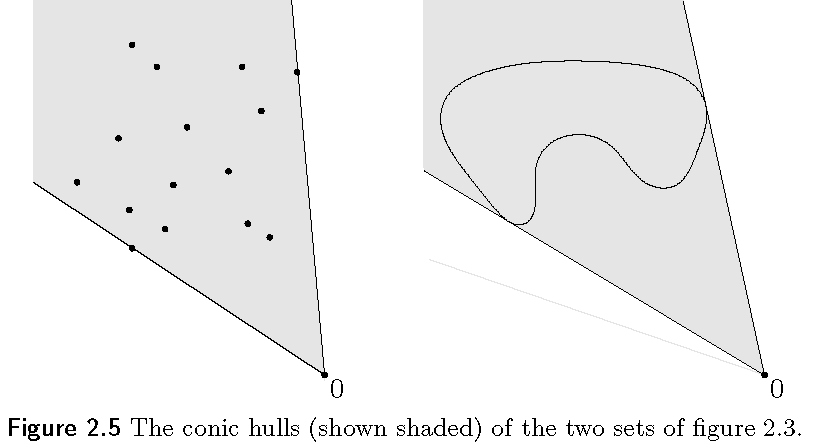
figure 2.5

一些想法

在我自己看来，在几何上
仿射集可以看成是集合中任意两个点的直线的集合。
凸集可以看成是集合中任意两个点的线段的集合，因为直线一定包含线段，所以仿射集一定是凸集。
锥集可以看成是集合中任意一个点和原点构成的射线的集合，锥集不一定是连续的（两条射线也是锥集），所以锥集不一定是凸集。
而凸锥既是凸集又是锥集。
我在stackexchange看到这样一句话觉得说的挺好的。

What basically distinguishes the definitions of convex, affine and cone, is the domain of the coefficients and the constraints that relate them.

区别凸集，仿射和锥的是系数的取值范围和一些其他限制。仿射集要求$\theta_1+\cdots+\theta_k = 1$，凸集要求$\theta_1 +\cdots +\theta_k = 1, 0\le \theta \le 1$，锥的要求是$\theta \ge 0$，凸锥的要求是$\theta_i \ge 0,i=1,\cdots,k$。
仿射集不是凸集的子集，凸集也不是仿射集的子集。所有仿射集的集合是所有凸集的集合的子集，一个仿射集是一个凸集。

示例

$\emptyset$，单点(single point)${x_0}$，整个$\mathbb{R}^n $空间都是$\mathbb{R}^n $中的仿射子集，所以也是凸集，点不一定是凸锥（在原点熵是凸锥），空集是凸锥，$\mathbb{R}^n $维空间也是凸锥。根据定义证明。
任意一条直线都是仿射的，所以是凸集。如果经过原点，它是一个子空间，也就是一个凸锥，否则不是。
任意一条线段都是凸集，不是仿射集，当它退化成一点的时候，它是仿射的，线段不是凸锥。
一条射线${x_0 + \theta v\big| \theta \ge 0}$是凸的，但是不是仿射的，当$x_0=0$时，它是凸锥。
任意子空间都是仿射的，也是凸锥，所以是凸的。

补充最后一条，任意子空间都是仿射的，也是凸锥。
如果$V$是一个子空间，那么$V$中任意两个向量的线性组合还在$V$中。即如果$x_1,x_2\in V$，对于$\theta_1,\theta_2 \in R$，都有$\theta_1 x_1 + \theta_2 x_2 \in V$。正如前面说的，子空间是加法和数乘封闭的。
而根据仿射集的定义，如果$x_1,x_2$在一个仿射集$C$中，那么对于$\theta_1+\theta_2 = 1$，都有$\theta_1 x_1 + \theta_2 x_2 \in C$。我们可以看出来，如果取子空间中线性组合的系数和为$1$，那么就成了仿射集。如果取子空间中的系数$\theta_1,\theta_2 \in R_+$,那么就成了锥，如果同时满足$\theta_1+\theta_2 = 1$，那么就成凸锥。那么如果加上这些限制条件，即取子空间中线性组合的系数和为$1$，或者取子空间中的系数$\theta_1,\theta_2 \in R_+$,同时满足$\theta_1+\theta_2 = 1$。
事实上，子空间要求的条件比仿射集和凸锥的条件要更严格。仿射集和凸锥只要求在系数$\theta_i$满足相应的条件时,有$\theta_1 x_1 + \theta_2 x_2 \in \mathbb{R}^n $；而子空间要求的是在系数$\theta_i$取任意值的时候，都有$\theta_1 x_1 + \theta_2 x_2 \in \mathbb{R}^n $，所以子空间一定是仿射集，也一定是凸锥。（拿二维的举个例子，给定$x_1$和$x_2$，仿射集可以看成是$\theta_1$的函数，因为$\theta_2=1-\theta_1$，而子空间可以看成$\theta_1$和$\theta_2$的函数，一个是一元函数，一个是二元函数）

超平面(hyperplane)和半空间(halfspace)

超平面是一个仿射集，也是凸集，但不一定是锥集(过原点才是锥集，也是一个子空间)。
闭的半空间是一个凸集，不是仿射集。

超平面(hyperplane)

超平面通常具有以下形式：
$${x\big|a^T x=b},$$
其中$a\in \mathbb{R}^n ,a\ne 0,b\in R$，它其实是一个平凡(nontrivial)线性方程组的解，因此也是一个仿射集。几何上，超平面可以解释为和一个给定向量$a$具有相同内积(inner product)的点集，或者说是法向量为$a$的一个超平面。常数$b$是超平面和原点之间的距离(offset)。
几何意义可以被表示成如下形式：
$${x\big|a^T (x-x_0) = 0},$$
其中$x_0$是超平面上的一点，即满足$a^T x_0=0$。可以被表示成如下形式：
$${x\big|a^T (x-x_0)=0} = x_0+a^{\perp},$$
其中$a^{\perp} $是$a$的正交补，即所有与$a$正交的向量的集合，满足$a^{\perp} ={v\big|a^T v=0}$。所以，超平面的几何解释可以看做一个偏移(原点到这个超平面的距离)加上所有垂直于一个特定向量$a$(正交向量)的向量，即这些垂直于$a$的向量构成了一个过原点的超平面，再加上这个偏移量就是我们要的超平面。几何表示如下图所示。
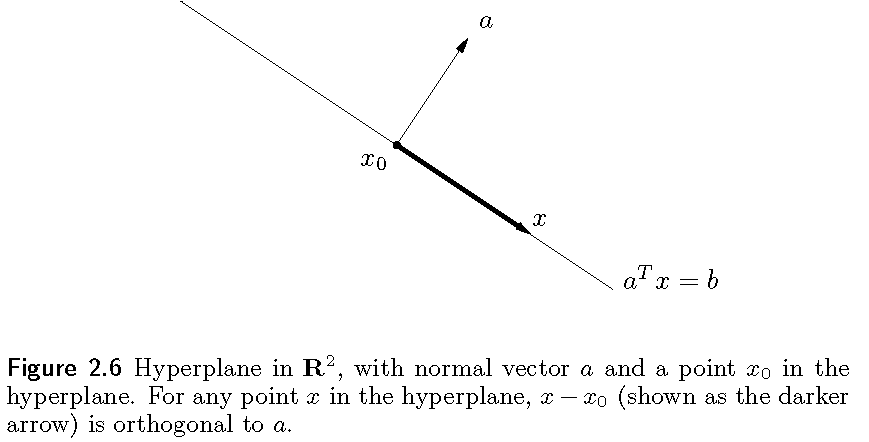
figure 2.6

半空间(halfspace)

一个超平面将$\mathbb{R}^n $划分为两个半空间(halfspaces)，一个是闭(closed)半空间，一个是开半空间。闭的半空间可以表示成${x\big|a^T x\le b}$，其中$a\ne 0$，半空间是凸的，但不是仿射的。下图便是一个闭的半空间。
figure 2.7
这个半空间也可以写成：
$${x\big|a^T (x-x_0)\le 0},$$
其中$x_0$是划分两个半空间的超平面上的一点，即满足$a^T x_0=b$。一个几何解释是：半空间由一个偏移$x_0$加上所有和一个特定向量$a$(超平面的外(outward)法向量)成钝角(obtuse)或者直角(right)的所有向量组成。
这个半空间的边界是超平面${x\big|a^T x=b}$。这个半空间${x\big|a^T x\le b}$的内部是${x\big|a^T x\lt b}$，也被称为一个开半平面。

欧几里得球(Euclidean ball)和椭球(ellipsoid)

欧几里得球

$\mathbb{R}^n $空间中的欧几里得球或者叫球，有如下的形式：
$$B(x_r,r = {x\big|\Vert x-x_c\Vert_2\le r}={x \big|(x-x_c)^T (x-x_c)\le \mathbb{R}^2 },$$
其中$r\gt 0$,$\Vert \cdot\Vert_2$是欧几里得范数(第二范数)，即$\Vert u\Vert_2=(u^T u)^{\frac{1}{2}} $。向量$x_c$是球心，标量$r$是半径。$B(x_c,r)$包含所有和圆心$x_c$距离小于$r$的球。
欧几里得球的另一种表示形式是：
$$B(x_c,r)={x_c + ru\big| \Vert u \Vert_2 \le 1},$$
一个欧几里得球是凸集，如果$\Vert x_1-x_c\Vert_2 \le r,\Vert x_2-x_c\Vert_2\le r, 0\le\theta\le1$，那么：
\begin{align*}
\Vert\theta x_1 + (1-\theta)x_2 - x_c\Vert_2 &= \Vert\theta(x_1-x_c)+(1-\theta)(x_2-x_c)\Vert_2\\
&\le\theta\Vert x_1-x_c\Vert_2 + (1-\theta)\Vert x_2 - x_c \Vert_2\\
&\le r
\end{align*}
用其次性和三角不等式可证明

椭球

另一类凸集是椭球，它们有如下的形式：
$$\varepsilon ={x\big|(x-x_c)^T P^{-1} (x-x_c) \le 1},$$
其中$P=P^T \succ 0$即$P$是对称和正定的。向量$x_c\in \mathbb{R}^n $是椭球的中心。矩阵$P$决定了椭球从$x_c$向各个方向扩展的距离。椭球$\varepsilon$的半轴由矩阵$P$的特征值$\lambda_i$算出，$\sqrt{\lambda_i}$，球是$P=\mathbb{R}^2 I$的椭球。
这里这种表示形式为什么要用$P^{-1} $？
椭球的另一种表示是：
$$\varepsilon = {x_c + Au\big| \Vert u \Vert_2 \le 1},$$
其中$A$是一个非奇异方阵。假设$A$是对称正定的，取$A=P^{\frac{1}{2}} $，这种表示就和上面的表示是一样的。第一次看到这种表示的时候，我在想，椭球的边界上有无数个点，一个方阵$A$是怎么实现对这无数个操作的，后来和球做了对比，发现自己一直都想错了，这无数个点是通过范数实现的而不是通过矩阵$A$实现的，到球心距离为$\Vert u\Vert_2\le 1$的点有无数个，$A$对这无数个点的坐标都做了仿射变换，将一个球变换成了椭球，特殊情况下就是球。当矩阵$A$是对称半正定但是是奇异的时候，这个情况下称为退化椭球(degenerate ellipsoid)，它的仿射维度和矩阵$A$的秩(rank)是相同的。退化椭球也是凸的。

范数球(norm ball)和范数锥(norm cone)

范数球(norm ball)

定义

$\Vert \cdot\Vert$是$\mathbb{R}^n $上的范数。一个范数球(norm ball)可以看成一个以$x_c$为中心，以$r$为半径的集合，但是这个$r$可以是任何范数，即${x\big|\Vert x-x_c \Vert \le r}$，它是凸的。

示例

我们常见的球是二范数（欧几里得范数）对应的范数球。

范数锥

定义

和范数相关的范数锥是集合：$C = {(x,t)\big|\Vert x\Vert \le t} \subset \mathbb{R}^{n+1} $，它也是凸锥。

示例

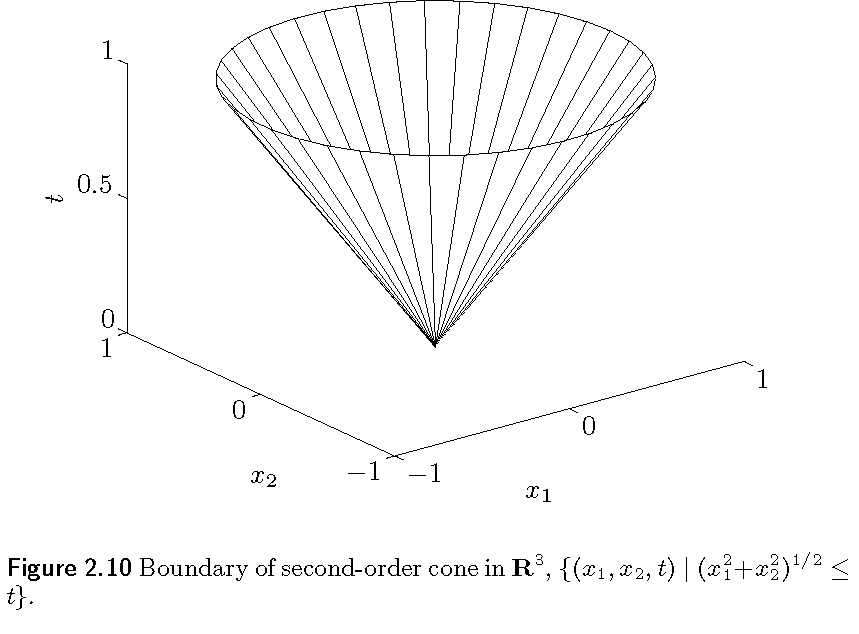
figure 2.10
二阶锥(second-order cone)是欧几里得范数对应的范数锥，如图所示，其表达式为：
\begin{align*}
C &={(x,t)\in \mathbb{R}^{n+1} \big| \Vert x\Vert_2 \le t}\\
&= \left{ \begin{bmatrix}x\\t\end{bmatrix} \big| \begin{bmatrix}x\\t\end{bmatrix}^T \begin{bmatrix}I&0\\ 0&-1\end{bmatrix} \begin{bmatrix}x\\t\end{bmatrix}\le 0, t \gt 0 \right}
\end{align*}
这个二阶锥也被称为二次锥(quadratic cone)，因为它是通过一个二次不等式定义的，也被叫做Lorentz cone或者冰激凌锥(ice-cream cone)。

范数锥和范数球的区别

范数球是所有点到圆心$x_c$的范数小于一个距离$r$。
范数锥是很多直线组成的锥。

多面体(polyhedra)

定义

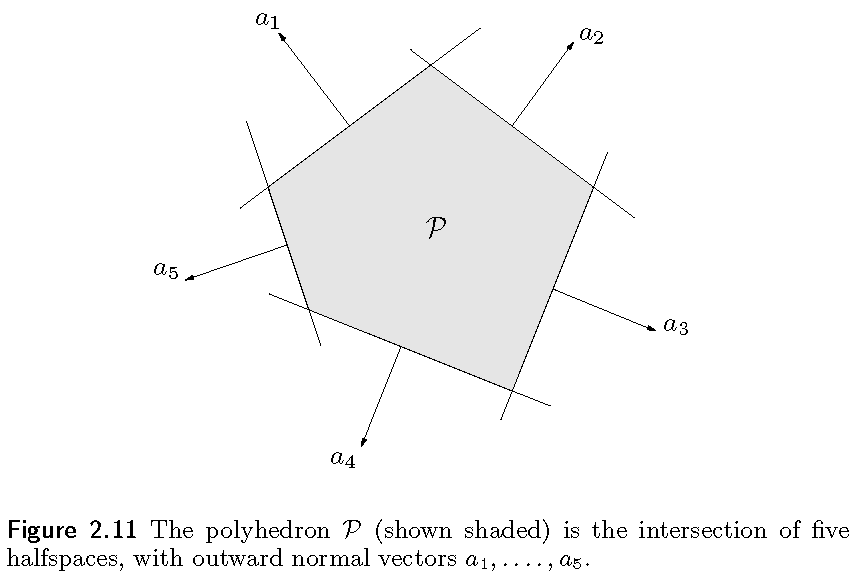
多面体(polyhedron)是有限个线性不等式或者线性方程组的解集的集合：
$P = {x\big|a_j^T x\le b_j, j=1,\cdots,m,c_j^T x=d_j,j=1,\cdots,p}$
多面体因此也是有限个半空间或者超平面的交集。仿射集(如，子空间，超平面，直线)，射线，线段，半空间等等都是多面体，多面体也是凸集。有界的polyhedron有时也被称为polytope，一些作者会把它们两个反过来叫。
上式的紧凑(compact)表示是：
$$P={x\big|Ax\preceq b, Cx=d}$$
其中$A=\begin{bmatrix}a_1^T \\ \vdots\\ a_m^T \end{bmatrix},C=\begin{bmatrix}c_1^T \\ \vdots\\c_p^T \end{bmatrix}$，$\preceq$表示$\mathbb{R}^m $空间中的向量不等式(vector ineuqalitied)或者分量大小的不等式，$u\preceq v$代表着$u_i\le v_i, i=1,\cdots,m$。

simplexes

simplexes是另一类很重要的多面体。假设$\mathbb{R}^n $空间中的$k+1$个点是仿射独立(affinely independent)，意味着$v_1-v_0, \cdots,v_k-v_0$是线性独立的。由$k+1$个仿射独立的点确定的simplex是：
$$C = conv{v_0,\cdots,v_k} = {\theta_0v_0+\cdots+\theta_kv_k\big| \theta \succeq 0, \mathcal{1}\theta=1 },$$
其中$\mathcal{1}$是全为$1$的列向量。这个simplex的仿射维度是$k$，所以它也叫$\mathbb{R}^n $空间中的$k$维simplex。为什么仿射维度是$k$，我的理解是simplex是凸集，而凸集不是子空间，凸集去掉其中任意一个元素才是子空间，所以就是$k$维而不是$k+1$维。
为了将simplex表达成一个紧凑形式的多面体。定义$y=(\theta_1,\cdots,\theta_k)$和$B=[v_1-v_0\ \cdots\ v_k-v_0]\in \mathbb{R}^{n\times k} $，当且仅当存在$y\succeq 0, \mathcal{1}^T y\le 1$，$x=v_0+By$有$x\in C$，疑问，这里为什么变成了$\mathcal{1}^T y\le 1$，难道是因为少了个$v_0$吗。点$v_0,\cdots,v_k$表明矩阵$B$的秩为$k$。因此存在一个非奇异矩阵$A=(A_1,A_2)\in \mathbb{R}^{n\times n} $使得：
$$AB = \begin{bmatrix}A_1\\A_2\end{bmatrix}B= \begin{bmatrix}I\\0\end{bmatrix}.$$
对$x = v_0+By$同时左乘$A$，得到：
$$A_1x = A_1v_0+y, A_2x=A_xv_0.$$
从中我们可以看出如果$A_2x=A_2v_0$，且向量$y=A_1x-A_1v_0$满足$y\succeq 0, \mathcal{1}^T y\le1$时，$x\in C$。换句话说，当且仅当$x$满足以下等式和不等式时：
$$A_2x = A_2v_0,A_1x\succeq A_1v_0, \mathcal{1}A_1x\le1+\mathcal{1}^T A_1v_0,$$
有$x\in C$。

多面体的凸包描述

一个有限集合${v_1,\cdots,v_k}$的凸包是：
$$conv{v_1,\cdots,v_k} = {\theta_1 v_1 +\cdots +\theta_k v_k\big| \theta \succeq 0, \mathcal{1}^T \theta = 1}.$$
这个集合是一个多面体，并且有界。但是它（除了simplex）不容易化成多面体的紧凑表示，即不等式和等式的集合。
一个一般化的凸包描述是：
$${\theta_1 v_1 +\cdots +\theta_k v_k\big| \theta_1+\cdots + \theta_m = 1,\theta_i \ge 0,i=1,\cdots,k}.$$
其中$m\le k$，它可以看做是点$v_1,\cdots,v_m$的凸包加上点$v_{m+1},\cdots,v_{k}$的锥包。这个集合定义了一个多面体，反过来，任意一个多面体可以看做凸包加上锥包。
一个多面体如何表示是很有技巧的。比如一个$\mathbb{R}^n $空间上的无穷范数单位球$C$：
$$C={x\big|\ |x_i|\le 1,i = 1,\cdots,n}.$$
集合$C$可以被表示成$2n$个线性不等式$\pm e_i^T x\le 1$，其中$e_i$是第$i$个单位向量。然而用凸包形式描述这个集合需要用至少$2^n $个点：
$$C = conv{v_{1},\cdots,v_{2^n }},$$
其中$v_{1},\cdots,v_{2n}$是$2^n $个向量，每个向量的元素都是$1$或$-1$。因此凸包描述和不等式描述有很大差异，尤其是$n$很大的时候。
这里为什么是$2^n $个点呢？因为是无穷范数构成的单位圆，在数轴上是区间$[-1,1]$，在$\mathbb{R}^2 $是正方形${(x,)\big|-1 \le x\le 1,-1\le y\le 1}$，对应的四个点是${(1,1),(1,-1),(-1,1),(-1,-1)}$，而在$\mathbb{R}^3 $是立方体${(x,y,z)\big|-1 \le x\le 1,-1\le y\le 1, -1\le z\le 1}$，对应的是立方体的八个顶点${(1,1,1),(1,1,-1),(1,-1,1),(1,-1,-1),(-1,1,1),(-1,1,-1),(-1,-1,1),(-1,-1,-1)}$。

示例

如图所示，是五个半平面的交集定义的多面体。
非负象限(nonnegative orthant)是非负点的集合，即：
$$R_{+}^n = {x\in \mathbb{R}^n \big| x_i\ge 0, i = 1,\cdots,n} = {x\in \mathbb{R}^n \big| x\succeq 0}.$$
非负象限是一个多面体，也是一个锥，所以也叫多面体锥(polyhedral cone)，也叫非负象限锥。
一个1维的simplex是一条线段。一个二维的simplex是一个三角形（包含它的内部）。一个三维的simple是一个四面体(tetrahedron)。
由$\mathbb{R}^n $中的零向量和单位向量确定的simplex是$n$维unit simplex。它是向量集合：
$$x\succeq 0, \mathcal{1}^T x \le 1.$$
由$\mathbb{R}^n $中的单位向量确定的simplex是$n-1$维probability simplex。它是向量集合：
$$x\succeq 0, \mathcal{1}^T x = 1.$$
Probability simplex是中的向量可以看成具有$n$个元素的集合的概率分布，$x_i$解释为第$i$个元素的概率。

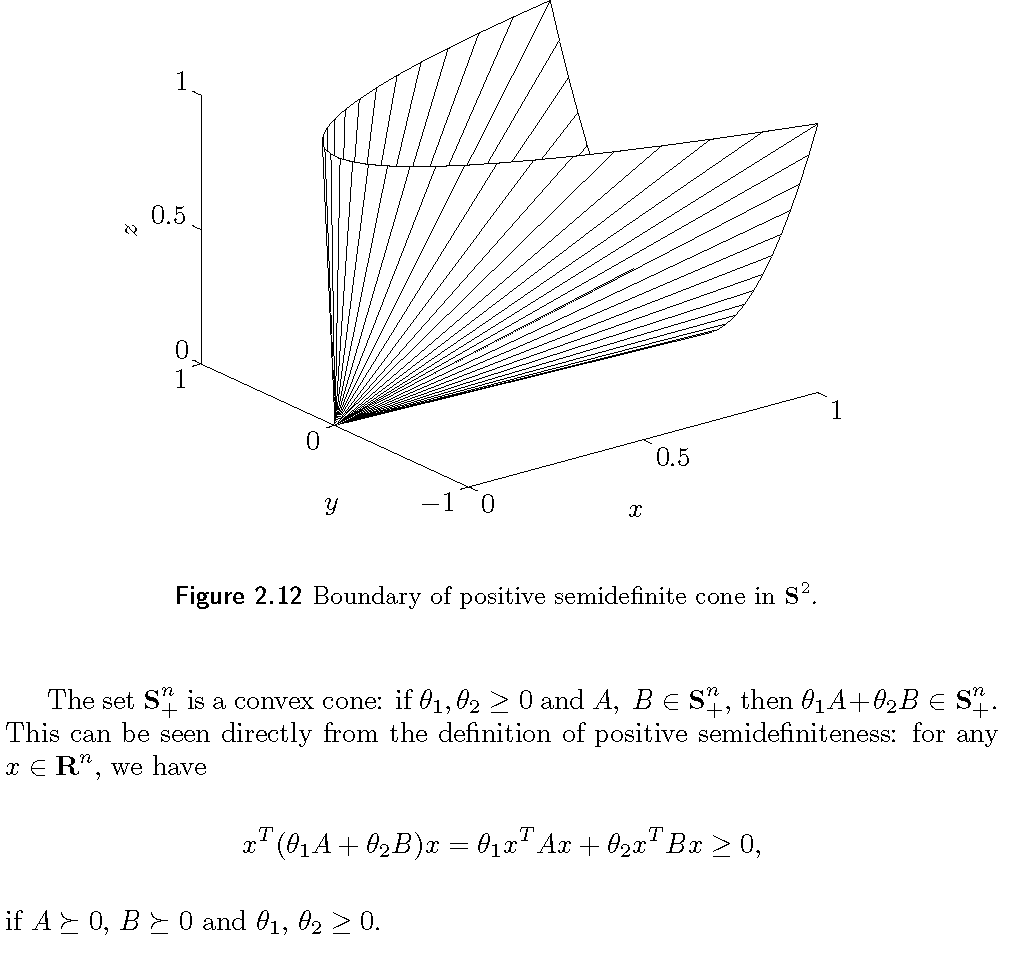
半正定锥(positive sefidefinite cone)

定义

用$S^n $表示$n\times n$的对称矩阵：$S^n ={X\in \mathbb{R}^{n\times n} \big| X = X^T }$，$S^n $是一个$n(n+1)/2$维基的向量空间。比如，三维空间中对称矩阵的一组基是：
$$\begin{bmatrix}1&0&0\\0&0&0\\0&0&0\end{bmatrix}\begin{bmatrix}0&0&0\\1&0&0\\0&0&0\end{bmatrix}\begin{bmatrix}0&0&0\\0&1&0\\0&0&0\end{bmatrix}\begin{bmatrix}0&0&0\\0&0&0\\1&0&0\end{bmatrix}\begin{bmatrix}0&0&0\\0&0&0\\0&1&0\end{bmatrix}\begin{bmatrix}0&0&0\\0&0&0\\0&0&1\end{bmatrix}.$$
用$S_{+}^n $表示半正定的对称矩阵集合：
$$S_{+}^n = {X\in S^n \big| X\succeq 0},$$
用$S_{++}^n $表示正定的对称矩阵集合：
$$S_{+}^n = {X\in S^n \big| X\succ 0},$$
集合$S_{+}^n $是凸锥：如果$\theta_1,\theta_2 \ge 0$且$A,B\in S_{+}^n $，那么$\theta_1 A+\theta_{2} B\in S_{+}^n $。这个可以直接从依靠半正定的定义来证明，如果$A,B\in S_{+}^n ,\theta_1,\theta_2\ge 0$，(这里原书中用的是$A,B\succeq 0$,我觉得应该是写错了吧)，对任意$\forall x \in \mathbb{R}^n $，都有：
$$x^T (\theta_1A+\theta_2B)x = \theta_1x^T Ax + \theta_2x^T Bx.$$

示例

对于$S^2 $空间中的半正定锥，有
$$X=\begin{bmatrix}x&y\\y&z\end{bmatrix}\in S_{+}^2 \Leftrightarrow x\ge 0,z\ge 0, xz\ge y^2 $$
这个锥的边界如下图所示。
figure 2.12

常见的几种锥

范数锥，非负象限锥，半正定锥，它们都过原点。
想想对应的图像是什么样的。
范数锥和非负象限锥图像还好理解一些，非负象限锥是$\mathbb{R}^n $空间所有非负半轴围成的锥，范数锥的边界像一个沙漏，但是是无限延伸的。半正定锥怎么理解，还没有太好的类比。

保凸运算(operations that preserve convexity)

这一小节介绍的是一些保留集合凸性，或者从一些集合中构造凸集的运算。这些运算和simplex形成了凸集的积分去确定或者建立集合的凸性。

集合交(intersection)

凸集求交集可以保留凸性：如果$S_1$和$S_2$是凸集，那么$S_1\cup S_2$是凸集。扩展到无限个集合就是：如果$\forall \alpha \in A,S_{\alpha}$都是凸的，那么$\cup_{\alpha\in A S_{\alpha}}$是凸的

仿射函数(affine functions)

线性分式(linear-fractional)和视角函数(perspective functions)

线性分式(linear-fractional)

视角函数(perspective functions)

广义不等式（Generalized inequalities)

真锥(Proper cones)和广义不等式（Generalized inequalities)

最小(Minimum)和最小元素(minimal elemetns)

Separating和supporting hyperplanes

Separating hyperplane theorem

Supporting Hyperplanes

对偶锥(dual cones)和广义不等式(generalized inequalities)

符号定义

$\preceq$表示$\mathbb{R}^m $空间中的向量不等式(vector ineuqalitied)或者element-wise的不等式，$u\preceq v$代表着$u_i\le v_i, i=1,\cdots,m$。

参考文献