Classfication
LDA
Logistic Regression
Logistic function
$$ S(x) = \frac{1}{1+e^{x} }$$
如下图所示:
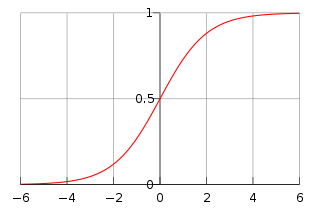
它的取值在$[0,1]$之间。
logistic regression的目标函数是:
$$h(x) = \frac{1}{1+e{-\thetaT x} 3}$$
其中$x$是输入,$\theta$是要求的参数。
思路
Logistic regression利用logistic function进行分类,给出一个输入,经过参数$\theta$的变换,输出一个$[0,1]$之间的值,如果大于$0.5$,把它分为一类,小于$0.5$,分为另一类。这个$0.5$只是一个例子,可以根据不同的需求选择不同的值。
$\theta^T x$相当于给出了一个非线性的决策边界。
Cost function
$$J(\theta) = -\log L(\theta) = -\sum_{i=1}^m (y(i)\log h(x^{(i)}) + (1-y{(i)})\log(1-h(x{(i)} )) )$$
给出两种方式推导logistic regression的cost function
Maximum likelyhood estimation
通过极大似然估计推导得到的,当是两个类别的分类时,即$0$或者$1$,有:
$$P(y=1|x,\theta) = h(x)$$
$$P(y=0|x,\theta) = 1- h(x)$$
服从二项分布,写成一个式子是:
$$P(y|x,\theta) = h(x)^y (1-h(x))^{1-y}$$
其中$y$取值只有$0$和$1$。
有了$y$的表达式,我们就可以使用最大似然估计进行求解了:
$$L(\theta) = \prod_{i=1}^m (h(x{(i)}){y(i)}(1-h(x^{(i)} )){(1-y{(i)})}$$
似然函数要求最大化,即求使得$m$个observation出现概率最大的$\theta$,
损失函数是用来衡量损失的,令损失函数取负的对数似然,然后最小化loss也就是最大化似然函数了:
$$J(\theta) = -\log L(\theta) = -\sum_{i=1}^m (y(i)\log h(x^{(i)}) + (1-y{(i)})\log(1-h(x{(i)} )) )$$
Cross-entropy
对于$k$类问题,写出交叉熵公式如下所示:
$$J(\theta) = -\frac{1}{n}\left[\sum_{i=1}^m \sum_k y_k^{(i)} \log h(x_k^{(i)} ) \right]$$
当$k=2$时:
$$J(\theta) = -\frac{1}{n}\left[\sum_{i=1}^m y^{(i)} \log h(x^{(i)} ) + (1-y^{(i)}) \log (1-h(x^{(i)} ))\right]$$
梯度下降
$$J(\theta) = -\log L(\theta) = -\sum_{i=1}^m \left[y(i)\log h(x^{(i)}) + (1-y{(i)})\log(1-h(x{(i)} )) \right]$$
\begin{align*}
\nabla J & = -\sum_{i=1}^m \left[ y(i)\frac{1}{h(x^{(i)})}\nabla h(x^{(i)}) - (1-y{(i)})\frac{1}{\log(1-h(x{(i)} ))}\nabla\log(1-h(x^{(i)} ))\right]
&=-\sum_{i=1}^m (h(x^{(i)}) - y^{(i)}) x^{(i)}
\end{align*}
参考文献
1.https://blog.csdn.net/jk123vip/article/details/80591619
2.https://zhuanlan.zhihu.com/p/28408516
3.https://www.cnblogs.com/pinard/p/6029432.html